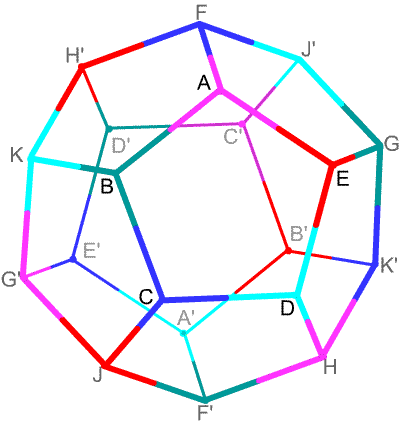

Figure 1. A regular dodecahedron has twelve faces, 20 vertices and 30 edges. Here $X,X'$ mark a pair of antipodal vertices. To create spherical dodecahedral space, we identify each face with its opposite after a twist of $\pi/10$ or $18^{\circ}$ to bring the vertices into congruence. So the face $ABCDE$ is identified with the face $C'D'E'A'B'$, etc. In particular, vertex $A$ is identified with $C'$, which is in turn identified with $H$, and then with $G'$. There are 5 sets of four vertices in the dodecahedron, each set corresponding to a single vertex in spherical dodecahedral space. Here they are distinguished by five different colors. Similarly edge $AB$ is identified with $C'D'$, which is then identified with $HF'$. There are 10 different color combinations, each corresponding to three edges in the dodecahedron, and to a single edge in spherical dodecahedral space. Finally the twelve faces are identified two by two. So spherical dodecahedral space has 5 vertices, 10 edges, 6 faces and one 3-dimensional cell which it inherits from the interior of the dodecahedron.
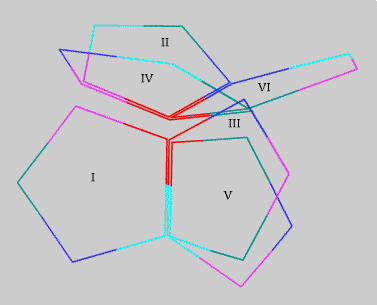
Figure 2. The four edges and six faces incident to the "red" vertex in spherical dodecahedral space. Here the faces (numbered I through VI) have been separated for legibility.
Spherical dodecahedral space as constructed here inherits a geometry from the dodecahedron. If one remains inside what was the 3-dimensional interior of the dodecahedron, geometrical calculations go exactly as they do in 3-dimensional Euclidean space; additionally, the faces themselves are not geometrically perceptible. The difference happens at the edges: they constitute a 1-dimensional singular set for the geometry. This is because the dihedral angle $\delta$ of a regular dodecahedron measures about $116.56^{\circ}$, so that around an edge, where three faces meet, the total angle is $3\delta$; and $3\delta$ is about $10.3^{\circ}$ less than $360^{\circ}$. Some space is missing. A 2-dimensional surface intersecting the boundary will have the geometry of a cone with central angle $3\delta$. In particular, the inhabitants of spherical dodecahedral space can measure the missing angle by drawing triangles enclosing the cone point.
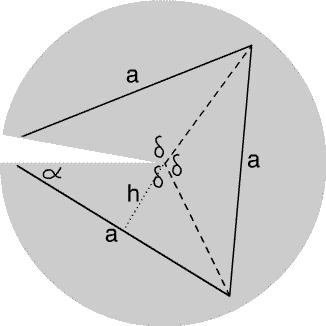
Figure 3. Using an equilateral triangle simplifies the
calculations. Here we draw one, of side length $a$,
around the cone point. For a calculation with plane geometry
the cone has been slit along a radius passing through a vertex of
the triangle. The central angle is $3\delta$ ($\delta$ the
dodecahedron dihedral); our triangle splits into three
isosceles triangles with angles $\delta, \alpha = (\pi-\delta)/2, \alpha$.
The sum of the interior angles of our triangle is $6\alpha =3(\pi-\delta)
= \pi + (2\pi-3\delta)$, i.e. greater by the "missing angle" than
the sum for a planar triangle.
The area is also larger. Each of the isosceles triangles
has base $a$ and altitude $h=(a/2)\tan\alpha$, so its
area is $(a^2/4)\tan\alpha$, giving $(3a^2/4)\tan\alpha$, about $.46a^2$,
for the
area of our
equilateral triangle. This is larger
than the area $a^2\sqrt{3}/4 \sim .43a^2$ of a planar
equilateral triangle with the same side
length.
An analogous discrepancy occurs around the vertices.
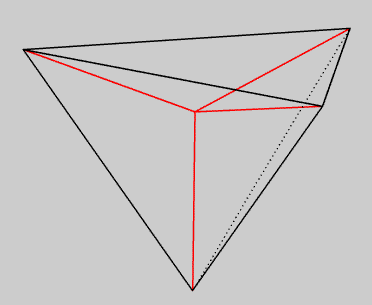
Figure 4. A regular tetrahedron drawn with one vertex on each of the four edges incident to the red vertex in spherical dodecahedral space.
When a regular tetrahedron is drawn with one vertex on each of the four edges incident to a space vertex, its volume breaks up as the sum of four equal pyramids. Each of them has an equilateral triangular base, and fits in a corner of the dodecahedron, so its three other faces are isosceles triangles with central angle the angle of a pentagon, i.e. $3\pi/5$.
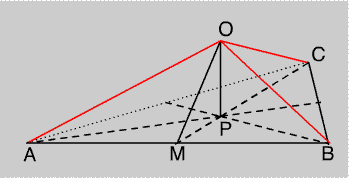
Figure 5. One of the four pyramids. $O$ is the space vertex, $A, B, C$ are equidistant from $O$, each on an edge incident to $O$. Angle $AOB = 3\pi/5$. Therefore angle $OAM = \pi/5$; setting length $AB=2a$ gives $OM= a\tan\pi/5$. $PM$ is one third of the altitude of the triangle, i.e. $a/\sqrt{3}$. The Pythagorean theorem then gives the height of the pyramid as $\sqrt{OM^2-PM^2}$ or $a\sqrt{ \tan^2\pi/5 -1/3}$, approximately $.44 a$. Since the area of the base is $a^2\sqrt{3}$, the volume of a pramid is about $.254a^3$ and the volume of the tetrahedron about $1.02a^3$. Compare this with the volume of a standard tetrahedron of side-length $2a$, which is $8a^3/6\sqrt{2}$, about $.94a^3$.
The fundamental group of a topological space was invented
by Poincaré; a simply connected space is one
with fundamental group equal to the identity.
For our purposes, let's suppose the space
is a generalized polyhedron with vertices, edges, faces and
3-dimensional cells. Choose a vertex, and look at all the
paths in the polyhedron which begin and end at that vertex.
Let's call such paths (based) loops.
Poincaré's idea was to consider this set as an algebraic
object, by taking the product of two loops $\ell_1$ and $\ell_2$ to be
the loop obtained by traversing first $\ell_1$ and then $\ell_2$.
This product does not define a group structure: it lacks an
identity element, and inverses. This can be remedied by replacing
loops with homotopy classes of loops: we identify two
loops if one can be continuously deformed into the other. Then
we can take the
the identity element to be the constant loop that never leaves the base vertex,
and the inverse of a loop to be the same loop traversed in the opposite
direction.

Figure 6. Five stages of a homotopy contracting to a constant path a loop that runs forward and backward along the same path.
The complete definition requires appropriate adjustments of parametrization, but this is, essentially, the fundamental group.In a polyhedron, any loop can be be deformed into a chain of
edges starting and ending at the base vertex; furthermore, if
one such loop can be deformed to another, the deformation itself can be
deformed into the 2-dimensional "skeleton" of the polyhedron: the
union of its vertices, edges and faces. This leads to a systematic
way of calculating the fundamental group of a polyhedron.
Here is how Seifert and Threlfall used that method to
compute the fundamental group of spherical dodecahedral
space. The calculation appears in their Lehrbuch der Topologie
(1934; English edition:
A Textbook of Topology, Academic Press, 1980).
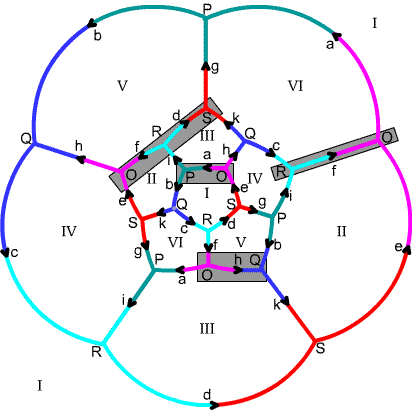
Figure 7. Auxiliary paths from basepoint vertex $O$ to the other four vertices. (This is the dodecahedron from Figure 1, flattened out so the back face corresponds to the outside of the figure, and with vertices and edges labeled by their equivalence classes.) Certain oriented edges (and a pair of edges) are singled out to serve as "auxiliary paths," and underlined in gray: $a$ leads from $O$ to $P$, $h$ from $O$ to $Q$, $f^{-1}$ from $O$ to $R$, and $f^{-1}d$ from $O$ to $S$.
Seifert and Threlfall label the five vertices of spherical dodecahedral space as $O,P,Q,R,S$, and choose vertex $O$ as the basepoint. They also label the ten edges $a, b, c, d, e, f, g, h, i, k$, oriented as shown in the picture, and label the six faces $I, II, III, IV, V, VI$ (this labeling also appears in Figure 2, above).The loops are labeled using the capitalized form of the edge labels (with $J$ for $i$). $$\begin{array}{|c|c|c|c|c|}\hline \mbox{edge}&\mbox{vertices}&\mbox{aux.}&\mbox{paths}&\mbox{loop}\\\hline a & OP & -& a& A=aa^{-1}\\\hline b & PQ & a& h& B=abh^{-1}\\\hline c & QR & h& f^{-1}& C=hcf^{-1}\\\hline d & RS & f^{-1}& f^{-1}d & D=f^{-1}d(d^{-1}f)\\\hline e & SO & f^{-1}d& - & E = f^{-1}de\\\hline f & OR & -& f^{-1} & F = f^{-1}f\\\hline g & SP & f^{-1}d& a & G=f^{-1}dga^{-1}\\\hline h & OQ & -& h & H=hh^{-1}\\\hline i & PR & a& f^{-1} & J=aif \\\hline k & QS & h& f^{-1}d & K = hk(d^{-1}f)\\\hline \end{array}$$
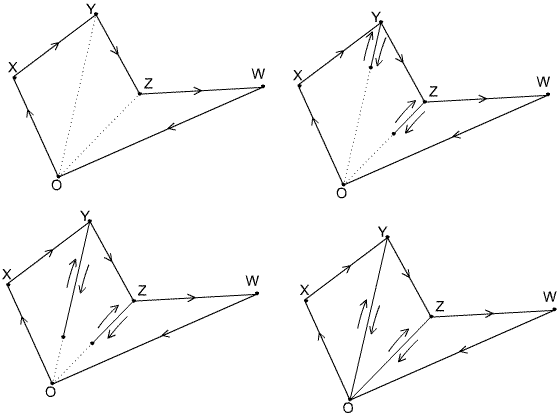
Figure 8. Four stages of a homotopy between a loop based at $O$ and a product of elementary loops: auxiliary path, edge (or edge$^{-1}$), auxiliary-path$^{-1}$.
This allows us to call the (homotopy classes of the) elementary loops $A, B, \dots K$ corresponding to the edges $a, b, \dots, k$ the generators of the fundamental group of spherical dodecahedral space.
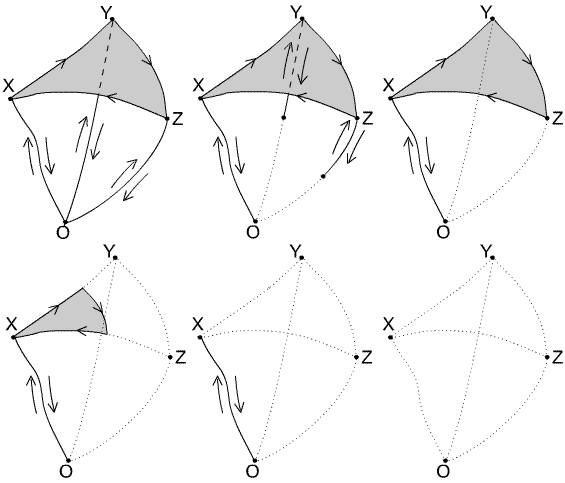
Figure 9. In this image, the 2-dimensional face is the triangle $XYZ$, $t$ is the edge $XY$, $u$ is $YZ$ and $v$ is $ZX$, oriented as written. Then $T$ is the loop $OXYO$, $U$ is $OYZO$ and $V$ is $OZXO$. If $x, y, z$ are the auxiliary paths $OX, OY, OZ$ then $T=xty^{-1}$, $U=yuz^{-1}$ and $V=zvx^{-1}$, so the product $TUV$ corresponds to the path $xty^{-1}yuz^{-1}zvx^{-1}$. The segments $y^{-1}y$ and $z^{-1}z$ can be shrunk to constant paths at $Y$ and $Z$, as was just done for relations of type I. This gives a homotopy between $TUV$ and the path $xtuvx^{-1}$. Then the face $XYZ$ supports the contraction of the segment $tuv$ to a constant path at vertex $X$, so $TUV$ is homotopic to $xx^{-1}$, a loop of type I; so $TUV=1$.
The fundamental group of spherical dodecahedral space is a group with two generators $B, U = BC^{-1}$ and the two relations $B^5 = (UB)^2=U^3$.
To show that the group is non-trivial, it is enough to show that the generating loops themselves are not homotopic to the identity. This can be done geometrically, by considering a small dodecahedral token placed in the center of the interior, parallel with the faces and labeled as the dodecahedron in Figure 1. We will concentrate on $B$.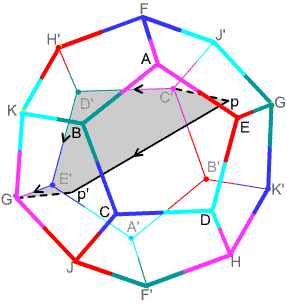
Figure 10. A circular path in spherical dodecahedral space: $pp'$ cycles through the center of face II ($BCJG'K = GK'B'C'J'$).
If the token dodecahedron is translated to $p'=p$ and back to the
center, it will have rotated $-\pi/5$ around the $pp'$ axis; if it
repeats the translation, it will have rotated $-2\pi/5$ around that
axis. This rotation realizes a
permutation of the vertices of the small dodecahedron,
corresponding to
$B\rightarrow C \rightarrow J \rightarrow G'
\rightarrow K \rightarrow B$,
$A\rightarrow D \rightarrow F' \rightarrow
E' \rightarrow H' \rightarrow A$,
$E \rightarrow H \rightarrow A' \rightarrow D'\rightarrow F \rightarrow E$,
$G\rightarrow K' \rightarrow B' \rightarrow C' \rightarrow J'
\rightarrow G$.
Since the circle $pp'$ traversed twice corresponds to a non-identity
permutation of the set of vertices of the token dodecahedron, it
follows that $pp'$ itself cannot be deformed to a constant path.
On the other hand, the grey surface in Figure 10 shows how $pp'$
can be deformed into the edge-path $C'D'E'G'$, which corresponds
to $abh^{-1}$, the loop $B$. If $B$ could be deformed to a constant
path, so could $pp'$; it follows that $B$ is a non-identity element
of the fundamental group of spherical dodecahedral space, and
therefore that spherical dodecahedral space is not simply
connected.
There is a different way of studying loops in a space: rather than defining equivalence in terms of deformation, one can define two oriented loops to be equivalent if together they form the boundary of a surface inside the space; we say that one is homologous to the other. If two loops are homotopic, like $pp'$ and $C'D'E'G'$ in Figure 10, then they bound an annulus like the grey surface in that figure. And if a loop can be shrunk to a point, the annulus collapses to a disk, so the loop bounds a disc.
Spherical dodecahedral space starkly shows the difference between the two classifications. There are loops like $B$ which cannot be shrunk to a point, but every loop is the boundary of a surface (of course, unless the loop is contractible, the surface cannot be a disk). Poincaré was able to deduce, using general machinery he had developed for studying homology in dimensions higher than one, that there is no homological way to distinguish spherical dodecahedral space from the 3-dimensional sphere.
This property of loops in spherical dodecahedral space can be proved algebraically, but it can also be understood geometrically. As an example, we will construct a surface in spherical dodecahedral space with boundary exactly equal to the edge path defining generator $B$.
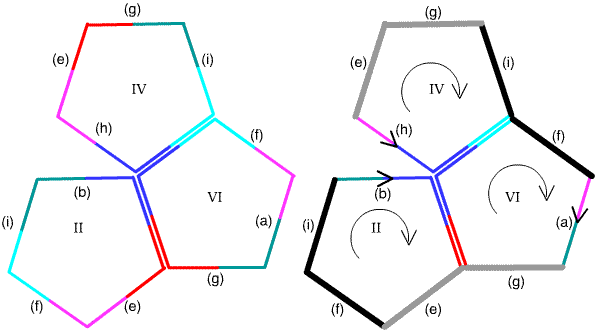
Figure 11. The faces II, IV, VI share several common sides. Identifying those sides leads to the polygon on the left, where further identifications need to be made between sides $(i),(f)$ and their duplicates, and between sides $(e),(g)$ and their duplicates. The first identification is shown in black on the right, the second in gray.
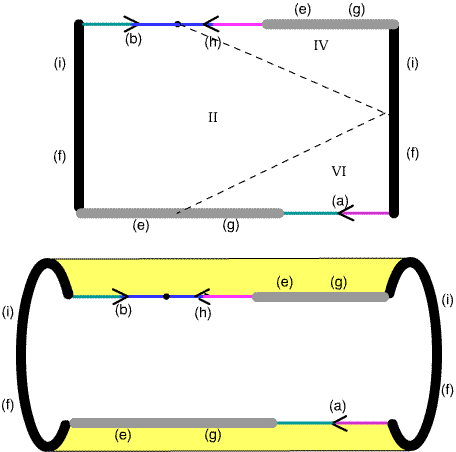
Figure 12. To visualize the effect of the identifications, we deform the union of faces II, IV, VI into a rectangle, maintaining the identity of the edges. The identification of $(e),(g)$ and their duplicates is accomplished in two steps. This is the first.
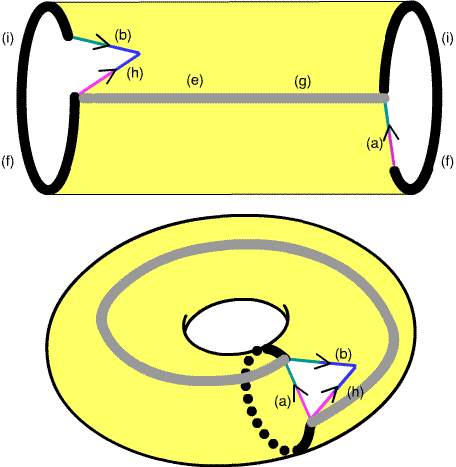
Figure 13. (Top) The $(e),(g)$ identification has been done; now the two $(i),(f)$ ends need to be identified. The result is a torus with a missing triangle: a surface whose boundary is the edge-path $abh^{-1}$ corresponding to the fundamental group generator $B$.
The 2-dimensional faces of spherical dodecahedral space are $$\begin{array}{|c|c|c|}\hline \mbox{face} & \mbox{edge-path} & \mbox{relation}\\\hline \mbox {I} & abcde & ABCDE=1\\\hline \mbox{II} & bkef^{-1}i^{-1} & BKEF^{-1}J^{-1}=1\\\hline \mbox{III} & aidk^{-1}h^{-1} & AJDK^{-1}H^{-1}=1\\\hline \mbox{IV} & ci^{-1}g^{-1}eh & CJ^{-1}G^{-1}EH=1\\\hline \mbox{V} & dgbh^{-1}f^{-1} & DGBH^{-1}F^{-1}=1\\\hline \mbox{VI} & cfag^{-1}k^{-1} & CFAG^{-1}K^{-1}=1\\\hline \end{array}.$$ In addition the type-I relations are $$\begin{array}{|c|c|c|}\hline \mbox{loop} & \mbox{edge-path} & \mbox{relation}\\\hline A & aa^{-1} & A=1\\\hline D & f^{-1}d (d^{-1}f) & D=1\\\hline F & f^{-1}f & F=1\\\hline H & hh^{-1} & H=1\\\hline \end{array}.$$ Substituting the second family into the first gives $$\begin{array}{|c|c|}\hline \mbox{face} & \mbox{relation}\\\hline \mbox {I} & BCE=1\\\hline \mbox {II} & BKEJ^{-1}=1\\\hline \mbox {III} & JK^{-1}=1; J=K \\\hline \mbox {IV} & CJ^{-1}G^{-1}E=1 \\\hline \mbox {V} & GB=1; B = G^{-1} \\\hline \mbox {VI} & CG^{-1}K^{-1}=1 \\\hline \end{array}.$$ Use III and V to eliminate $G$ and $K$: $$\begin{array}{|c|c|}\hline \mbox{face} & \mbox{relation}\\\hline \mbox {I} & BCE=1; E = C^{-1}B^{-1}\\\hline \mbox {II} & BJEJ^{-1}=1\\\hline \mbox {IV} & CJ^{-1}BE=1 \\\hline \mbox {VI} & CBJ^{-1}=1; J=CB \\\hline \end{array}.$$ Usee I and VI to eliminate $E$ and $J$: $$\begin{array}{|c|c|}\hline \mbox{face} & \mbox{relation}\\\hline \mbox {II} & BCBC^{-1}B^{-2}C^{-1}=1\\\hline \mbox {IV} & CB^{-1}C^{-1}BC^{-1}B^{-1}=1 \\\hline \end{array}.$$ Now insert $1=CB^{-1}C^{-1}BC^{-1}B^{-1}$ (from IV) after the fourth factor in II: $$\begin{array}{|c|c|}\hline \mbox{face} & \mbox{relation}\\\hline \mbox {II & IV} & BCBC^{-1}CB^{-1}C^{-1}BC^{-1}B^{-1}B^{-2}C^{-1}=1\\\hline \mbox {IV} & CB^{-1}C^{-1}BC^{-1}B^{-1}=1 \\\hline \end{array}.$$ Simplify: $$\begin{array}{|c|c|}\hline \mbox{face} & \mbox{relation}\\\hline \mbox {II & IV} & B^2C^{-1}B^{-3}C^{-1}=1\\\hline \mbox {IV} & CB^{-1}C^{-1}BC^{-1}B^{-1}=1 \\\hline \end{array}.$$ Let $U = BC^{-1}$ (i.e. $C=U^{-1}B$, $C^{-1}=B^{-1}U$): $$\begin{array}{|c|c|}\hline \mbox{face} & \mbox{relation}\\\hline \mbox {II & IV} & B^2B^{-1}UB^{-3}B^{-1}U=1\\\hline \mbox {IV} & U^{-1}BB^{-1}B^{-1}UBB^{-1}UB^{-1}=1 \\\hline \end{array}.$$ Simplify: $$\begin{array}{|c|c|}\hline \mbox{face} & \mbox{relation}\\\hline \mbox {II & IV} & BUB^{-4}U=1;~~~ B^4 = UBU;~~~B^5 = (UB)^2\\\hline \mbox {IV} & U^{-1}B^{-1}U^2B^{-1}=1;~~~ U^2 = BUB;~~~U^3 = (UB)^2 \\\hline \end{array}.$$ Finally: the fundamental group of spherical dodecahedral space is a group with two generators $B, U$ and the two relations $B^5 = (UB)^2=U^3$.