In 1965 my late friend and colleague John Stallings wrote "How not to prove the Poincaré conjecture." This work appeared in the Proceedings of the Wisconsin Topology Seminar and is still available on John's Berkeley website. It begins with the declaration: "I have committed the sin of falsely proving Poincaré's Conjecture. But that was in another country; and besides, until now no one has known about it." It continues with the exposition of the main ideas relating the conjecture to statements in Algebra, and is certainly what Stephen Miller had in mind when he wrote, in the AMS Notices, after John's death, "His 1960s papers on the 3-dimensional Poincaré Conjecture are both brilliant and hilarious at the same time."
In 1445 Nicholas of Cusa wrote De Geometricis Transmutationibus (On Geometric Transmutations); my account is based on a recent translation into French of all of Nicholas' mathematical works: Nicolas de Cues, Les Écrits mathématiques by Jean-Marie Nicolle (Honoré Champion, Paris, 2007). This was the first of Cusa's writings in which he addressed the problem of squaring the circle. Literally, squaring the circle means devising the straightedge-and-compass construction of a square whose area equals that of a given circle. This means a construction relating a segment of length 1 (the radius of the circle) to a segment of length $\sqrt{\pi}$ (the side of the square). Nicholas's plan was start from an equilateral triangle and construct an isoperimetric circle; this is the content of the First Premise in De Geometricis Transmutationibus. If the triangle had perimeter 1, the circle would have diameter $1/{\pi}$. Then the composition of two more standard straight-edge and compass constructions could start from that diameter and generate first a segment of length $\sqrt{1/\pi}$, and from that one a segment of the reciprocal length $\sqrt{\pi}$.
 |
 |
Examples of straight-edge and compass arithmetic:
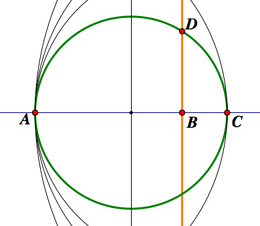
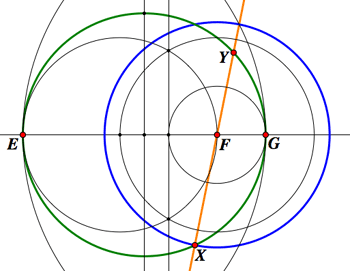
Left: square root. A segment $AB$ of length $x$ is extended by
a segment $BC$ of length 1. Choose one of the points $D$ where
the (green) circle with diameter $AC$
intersects the perpendicular through $B$. Then by plane geometry
$DB^2 = AB\cdot BC = AB$, so $DB$ has length $\sqrt{x}$.
Right: reciprocal. The construction starts with a segment $EF$
of length 2 extended by $FG$ of length $\frac{1}{2}$. A circle (green)
is constructed with $EG$ as diameter. For any $x$ between $1/2$
and 2, for example $\sqrt{1/\pi}$, a circle (blue) of radius $x$ is drawn with
center $F$. Choose one of the intersection points $X$ of the two
circles and draw the line
through $X$ and $F$. It will intersect the green circle at a second point $Y$;
the length $y$ of the segment $FY$ will be the reciprocal of $x$,
since by standard plane geometry
$XF\cdot FY = EF\cdot FG = 1$.
Other circles, lines and points used in the constructions are shown in black.
Nicholas of Cusa (1401-1464) was one of the leading intellectual figures in early 15th-century Europe. He is often described as a transitional figure between the Middle Ages and the Renaissance, and in fact he was personally involved in one of the great events that mark that transition: Pope Eugene IV sent him to Constantinople in 1437 as part of a delegation to negociate the participation of the Eastern Orthodox hierarchy in the Council of Florence. They came, with an entourage of distinguished Greek scholars who stayed, and lectured, in Florence; contributing to the surge of interest in humanistic learning which led to the new age.
Nicholas' principal occupations were ecclesiastical politics and administration (he was named Cardinal in 1449) and, relatedly, theology/philosophy. Those were a tumultuous times for the Church; Nicholas was at the center both of bitter jurisdictional controversies and of intense disputation about the exact wording of dogmatic texts, where the placement of a comma could assume cosmic importance. In those days philosophy, theology and natural science were closely linked: the physical structure of the universe had deep theological implications. Nicholas' energetic and erudite mind, in a priori meditation, led him to scientific insights that turned out to be prophetic. For example, he understood that the earth, the sun and the moon were objects moving through space; and he rejected the idea that all orbits had to be circular or even that the universe had a center (De Docta Ignorantia, Book II). Here he was a predecessor of Kepler (who referred to him as "divine") and of Giordano Bruno.
Nicholas' interest in mathematics seems to have been its status as an impregnable logical system. He believed that by testing his philosophical theories in mathematics he could produce convincing evidence of their validity. He outlines the parallelism between geometry and theology in De Circuli Quadratura, dated July 1450. "Transport yourself by assimilation from these mathematics to theology. ... Just as the circle is perfection in a figure, since any perfection of figures is worked into it, its surface contains all the surface of all figures and has nothing in common with all the other figures, but is absolutely one and simple in itself; likewise absolute eternity is the form of all forms ... having nothing in common with any other form. And whatever the figure of the circle therein may be, since it has neither beginning nor end, it has resemblance with eternity ... . ... Likewise, if a triangle wanted to triangulate the circle, or a square to square it and so forth for the other polygons, thus also intellectual nature wants to understand [God]."
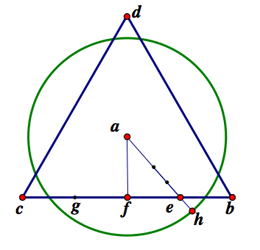
Nicholas of Cusa's First Premise: $a$ is the center of the equilateral triangle $bcd$. "You divide the side $bc$ into four equal parts which you mark $e, f, g$: I assert that, if one extends the line drawn from $a$ to $e$ by its fourth, which gives $ah$, this will be the radius of the circle whose circumference is equal to the three sides of the triangle."
One of the thought schemata Nicholas devised for use in theology was the
"concidence of opposites." Here is how he applied the principle
to the proof of his First Premise.
The construction involves a parameter, namely the position of
the point $e$ on the line $cb$. Nicholas observes that when
$e$ is at the midpoint $f$ the length of the segment $ah$
is smaller than the desired radius, and that when $e$ is at $b$
the length is larger. He applies the principle: ubi est dare
magis et minis, quod ibi sit dare aequale (where one can give
a greater and a lesser, one can also give an equal; essentially
the intermediate value theorem) and
concludes correctly that for some intermediate position
$x$ the length $ah$ must be exactly equal to that radius,
"and that is the point $e$ equidistant between $b$ and $f$."
The last statement made with no justification.
The construction is in fact plausible:
suppose the sides of the triangle have length 1.
Then $ef = \frac{1}{4}$; similarity of triangle
$abf$ with a half-equilateral triangle, and the Pythagorean
theorem, yield $af = \frac{1}{2\sqrt{3}}$;
so $ae = \sqrt{\frac{7}{48}}$,
and $ah = (5/4)\sqrt{\frac{7}{48}}$; the First Premise
states that $2\pi\cdot ah = 3$, which implies
$\pi = \frac{6}{5}\sqrt{\frac{48}{7}} = 3.1423...$ . This value, which Nicholas
could have calculated but never mentions explicitly, was within the
bounds $[\frac{223}{71}, \frac{22}{7}] = [3.14084... , 3.14285...]$ established by
Archimedes. Therefore, until better approximations to
$\pi$ were available, there was no way to prove Nicholas's
construction wrong, even though there were obvious gaps
in his proof.
Nicholas circulated copies of his work among his friends, who included Paolo Toscanelli (1397-1482), a Florentine astronomer and physician. He had been a classmate of Nicholas', and they remained good friends for life. Toscanelli wrote back with objections. To us, now, it is clear that there was no way the argument could be repaired. Nicholas' solution was to devise a different, and considerably more complicated, construction.
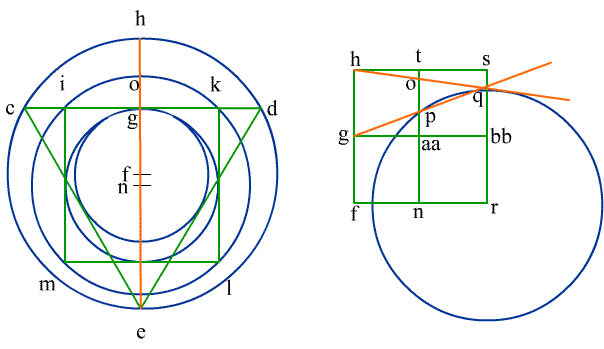
The diagram for Nicholas of Cusa's second quadrature construction, from Quadratura Circuli, 1450. The construction starts from a triangle $cde$, superimposes an isoperimetric square $ilkm$ and yields $rq$ as the radius of the isoperimetric circle.
Nicholas would have done better to stay with his first construction. The new one was reprinted and minutely analyzed by Regiomontanus (Johannes Müller, 1436-1476) who showed that the implied value for $\pi$ was outside the Archimedean bounds (Nicolle calculates it as 3.154); this is part of a 60-odd page appendix to his De triangulis omnimodis, dated 1464, published in 1533. There Regiomontanus takes up all of Nicholas' constructions one by one and "does the math" (Nunc ad numeros descendendum), using his knowledge of trigonometry to show "that Nicholas' approximations to $\pi$ were --except one-- not even within the limits established by Archimedes," according to Menso Folkerts, who characterizes Regiomontanus as "a gifted student of Archimedes," and Nicholas of Cusa as "an amateur in mathematics." The one exception is presumably the First Premise above.Nicholas of Cusa was attacking a problem dating back to the ancient Greeks. The solution would have made him famous forever, and might even have helped bolster his side in theological disputations. No one knew at the time that squaring the circle is impossible: the proof requires calculus, which was 200 years away; and even then it was not discovered until 1882.
John Stallings was also attacking a famous problem: 50 years old, a very long time in modern mathematics. In this case the problem was not impossible, but the methods that led to its solution lay far in the future. Richard Hamilton's introduction of the Ricci flow, which led to Gregory Perelman's ultimate victory, came out in 1982, some 17 years after Stallings wrote "How not to prove the Poincaré Conjecture." But Stallings discovered his error by himself, before publishing, whereas Nicholas seems to have believed until the end that he had squared the circle, but perhaps had not been able to find the right argument to substantiate his claim.
Here is how Stallings ends his story: "... I was unable to find flaws in my 'proof' for quite a while, even though the error is very obvious. It was a psychological problem, a blindness, an excitement, an inhibition of reasoning by an underlying fear of being wrong. Techniques leading to the abandonment of such inhibitions should be cultivated by every honest mathematician."
We will see that any length occurring in a compass and straight-edge construction starting from length one must be an algebraic number, i.e. it must be a root of a polynomial with integer coefficients. Considerably more intricate is the proof that $\pi$, and therefore $\sqrt{\pi}$, is transcendental, i.e. not algebraic. Some references are given here.
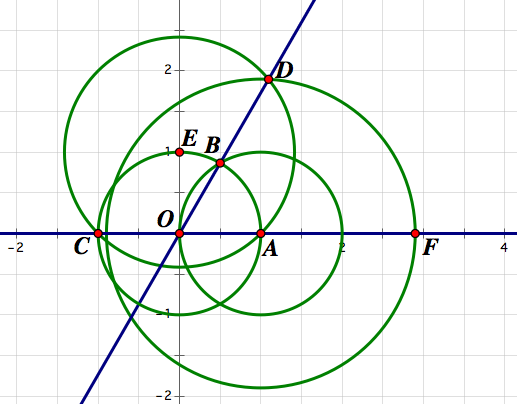
A random compass-straightedge construction: all the coordinates of the vertices produced by the construction are of a special form: they are obtained from 1 by composing a finite number of operations, which can be arithmetic (sum, product, quotient, etc.) or the extraction of a square root. For future use, let's call the set of these numbers S. In this example, the construction starts with the vertices $O = (0,0)$ and $A = (1,0)$; line they span is the $x$-axis. The circle of center $O$ and of radius $OA$ intersects the circle of center $A$ and of radius $OA$ at $B = (\frac{1}{2}, \frac{\sqrt{3}}{2})$, the $x$-axis at $C = (-1,0)$ and the $y$-axis (the perpendicular bisector of $AC$, constructed as usual by two circles and a line) at $E = (0,1)$. The circle of center $E$ and radius $EA$ intersects the line through $O$ and $B$ at $D = (\frac{\sqrt{3} + \sqrt{7}}{4}, \frac{3+\sqrt{21}}{4})$. The circle of center $A$ and radius $AD$ intersects the $x$-axis at $F = (1 + AD,0) = (1 + \frac{1}{2}\sqrt{7 + \sqrt{21} - \sqrt{3} -\sqrt{7}}, 0).$ As the construction continues, the number of embeddings of radicals into radicals tends to rise, but the numbers always have this general form. They are clearly algebraic, since the radicals can be peeled off by continued squaring and rearranging. In fact these constructible numbers form a special class of algebraic numbers: those that can be reached from the rational numbers by a finite number of quadratic extensions, i.e. by arithmetic operations and taking square roots a finite number of times. To show squaring the circle is impossible, "algebraic" is sufficient; but other impossibilities (duplicating the cube, trisecting the angle) require this additional information.
Menso Folkerts, "Regiomontanus' role in the transmission and transformation of Greek mathematics," in Tradition, transmission, transformation: proceedings of two Conferences on Pre-Modern Science held at the University of Oklahoma, ed. by F. Jamil Ragep and Sally P. Ragep. With Steven Livesey. Leiden; New York; Köln; Brill 1996.