This month's topics:
Calculus in Babylon?
"Signs of Modern Astronomy Seen in Ancient Babylon" was the title
for Kenneth Chang's article in the
New York Times, January 28, 2016. Other science writers
were more daring.
"Ancient Tablet Shows Babylonians Used Calculus to Track Planets"
(Devin Coldewey, NBC News, Jan. 29), "Ancient Babylonians used early calculus to track path of Jupiter, study finds" (Steve Connor, Independent, Jan. 28) and even the absurd "Ancient Babylonian astronomers used calculus to find Jupiter 1,400 years before Europeans" (Start Gary, ABC Science,
Jan. 29). The study in question is in fact unambiguously titled:
"Ancient Babylonian astronomers calculated Jupiter's position from the area under a time-velocity graph" (Science, Jan. 29); the author is
Mathieu Ossendrijver, Humboldt University, Berlin.

Babylonian
Tablet BM 40054 (approximately 4.5 cm wide),
previously unpublished and dated 350-50 BCE, is Ossendrijver's "Text A".
Ossendrijver's line by line translation:
- The day when it appears: 0;12, until 1,0 days, 0;9,30.
- 0;12 and 0;9,30 is 0;21,30, times 0;30
- is 0;10,45, times 1,0 is 10;45.
- After completing 1,0 days, until 1,0 days 0;1,30.
- 0;9,30 and 0;1,30 is 0;11, times 0;30 is 0;5,30.
- 0;5,30 times 1,0 days is 5;30. (erasure) 10;45 and 5;30 is
- 16;15, the total. From appearance until station the motion is 16;15
Image credit: Trustees of the British Museum, Mathieu Ossendrijver, used with permission (larger image).
The numbers in the caption are transcribed in Babylonian base-60 notation,
so 0;12 = 0.210, 1,0 = 6010, 0;9,30 =
9/60 + 30/3600 = 0.15810, etc.
This tablet had been classified as a mathematical problem text until
Ossendrijver noticed that it matched partial
calculations on several other inscrutable
tablets, two of which mention Jupiter
explicitly (all of these tablets
had been sitting in the British Museum
since around 1880). By collating them he was able to arrive at an
almost complete
understanding of all of the calculations.
What is remarkable is that the Babylonian astronomers
of that period understood that the adding up of
daily increments of displacement to give total displacement was
mathematically the same as adding up the areas of constant-width strips
to give the total area of a trapezoid. The area of a
trapezoid is $\frac{1}{2} (\mbox{base} + \mbox{top})\times \mbox{height}$.
The first three lines of Text A give a parallel calculation for
the displacement of Jupiter over a 60-day period. The first
day's displacement is 0;12 (=0.210), the displacement
on day 60 is 0;9,30 = 0.15810. You add 0;12 to 0;9,30
to get 0;21,30 = 0.358..10 which you multiply by 0;30 =
$\frac{1}{2}$ to get 0;10,45 = 0.179..10 which is then
multiplied by 1,0 = 6010 to give a total displacement
10;45 = 10.7510.
Another calculation (reconstructed by Ossendrijver
from fragments on the other tablets) further substantiates the
Babylonians' conflation of displacement and area calculations: to
reckon the date at which Jupiter would have gone half-way between
its positions at day 1 and at day 60, they used the
geometric formula (known to them since Old Babylonian times)
giving the length and position
of a horizontal slice cutting a trapezoid into two of
equal area [the length is $\sqrt{\frac{1}{2}(\mbox{base}^2 +
\mbox{top}^2)}$ ].
Truchet train-tracks at the Museum of Mathematics.
Kenneth Chang's story ran in the New York Times on February 1, 2016: "At Museum of Mathematics, Meet 2 Beavers That'll Never Meet." It's
about a new exhibit at the Museum, but mainly about how it was thought
up and how hard it was to make it work. What visitor's see is a model
train layout with very loopy track running through what looks like
swampy, woodsy territory. Two beavers, separately, wind their way along
the track. Now this is a special track: there are 24 turntables which
visitors can activate to change the configuration of the layout. It can be
one large loop (in several ways), 18 small loops and almost anything
in between. But
as Chang's title suggests, no matter how the track is changed, the
beavers can never collide.
"The exhibit grew out of brainstorming about
Truchet tiles, named after Sébastien Truchet, a French Dominican priest who described them in 1704." More about Truchet tiles.
"The Beaver Run exhibit is based on Truchet tiles popularized in 1987 by Cyril Stanley Smith, a scientist at Massachusetts Institute of Technology. On each tile, two quarter-circles connect midpoints of adjacent sides."
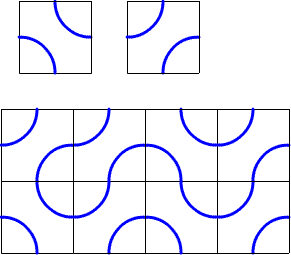
Truchet tiles with quarter-circle markings,
and part of a typical tiling.
"Timothy Nissen, the museum's chief designer, thought of turning the quarter-circles into train tracks." And of rearranging them remotely by
making interior tiles into turntables which, when rotated
90$^{\circ}$, change one layout to another.

One configuration of a
layout with $2\times 3$ turntables.
Glen Whitney, the Museum founder and president, "also a model train enthusiast, liked the idea, and he remembered the mathematical proof that would allow two trains to run on the tracks and never crash." (The rules specify that a
turntable cannot be rotated if there's a train on it).
The proof runs like this. First, the layout can
be arranged so that all the track forms a single loop (any two adjacent
loops can be joined by rotating a shared turntable). Use that loop to
put a "forward" direction on the whole track.
Now observe that if any single turntable is rotated, the new
layout is compatible with the global forward direction.
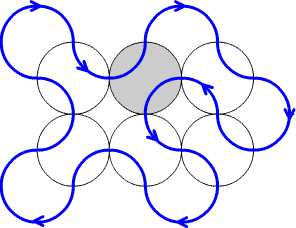
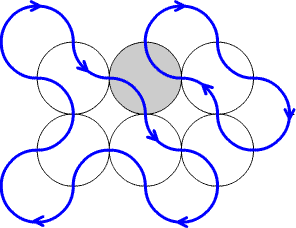
Here the layout has a single loop, and a
forward direction has been recorded.
Rotating the shaded turntable gives a new
layout with the same overall forward direction.
It follows that if the two trains are started
going in the same direction, they will always go in the same
direction. And if they travel at the same constant speed,
one can never catch up with the other.
Chang shares with us the secret of how Nissen and Whitney's
locomotives and cars got morphed into beavers
destined never to meet. He quotes Cindy
Lawrence, co-Director of the Museum:
"I had a very strong sense that trains might appeal more to boys than girls.We thought little beavers, little animals, are more universally appealing."
Who Needs Advanced Math? Not Everybody.
This was the title of an "Ed Talk" interview that ran in
the Education Life section of the New York Times on
February 7, 2016. Jane Karr interviewed Andrew Hacker, who
after teaching political science (Queens College, CUNY) for
nearly 45 years has branched out into quantitative reasoning
for the last three. "His experimental course requires no geometry, algebra or calculus; instead, he teaches facility with numbers. He calls it adult arithmetic, and it involves statistics, analytic thinking and rigorous computation. Further challenging convention, his new book, The Math Myth and Other STEM Delusions, published next month, argues against the requirement that all high school students take a full menu of math." (Link to coverage here of his
2012 Op-Ed on the topic.) Some excerpts from
Hacker's answers:
- At the very time we should be honing and sharpening quantitative reasoning skills we punch students into algebra, geometry, calculus. The Math People take over and ignore much simpler needs. Arithmetic is super essential -- we quantify everything.
- One in five of our ninth graders fails to get a high school diploma, and the single biggest academic reason is that they fail math. And this is getting worse with the Common Core. A CUNY study of its mandated algebra course found that 57 percent failed.
- [Aren't algebra and geometry essential skills?]
The number of people who use either in their jobs is tiny, at most 5 percent. You don't need that kind of math for coding. It's not a building block.
Colleges do require math to get in, much more than their students will need. It's a "rigor" ritual that makes them feel better about themselves.
- On the whole, I'd be happy if the ACT and SAT quietly disappeared. Speed may be necessary for firefighters and airline pilots. But not in the intellectual enterprise. And yet, on many fronts, test scores in math provide an edge for awards and admissions.
An answer to Prof. Hacker came in a letter to the Times published
on February 19, from Lucy Brownstein in Brooklyn.
- Andrew Hacker ...
says that since only 5 percent of people use algebra and/or geometry
in their jobs, students don't need to learn these subjects.
As a high school student, I strongly disagree.
The point of learning is to understand the world.
If the only point of learning is job preparation, why should students
learn history, or read Shakespeare?
And while your job may never require you to know
the difference between a postulate and a theorem, it will almost
certainly require other math-based skills, like how to prove
something, or how to understand a graph. ...
Algebra and geometry have a place in the classroom.
If students are failing, then the way math is taught may need to
change. But what is taught needs no alteration.
A similar interview appears in the Chronicle
of Higher Education, February 26: "The Case Against Mandating Math
for Students," interviewer Dan Berrett. The occasion is the upcoming
publication of The Math Myth ... .
Barrett summarizes the argument: "Typical math requirements, like mastering polynomial functions or parametric equations, unnecessarily trip up students who plan to major in dance or fashion design ... and are seldom used even in many scientific disciplines. Arithmetic, on the other hand, is the quantitative literacy that people actually need. But it's often poorly focused and poorly taught."




