Math in the Media 0502

Math in the Media

June 2002

Moving with VIGRE
A new kind of science?
Math teachers with no math
New / old math probes the big bang
A differential equation for organism growth
Trig tables in verse

$*$ Moving with VIGRE. Vertical Integration of Research and Education is a 4-year old NSF program aimed improving the way higher mathematics education works in the United States. It's the focus of ``NSF Moves With VIGRE to Force Changes in Academia'' by Dana Mackenzie, in the May 24 2002 Science. The idea is to structure mathematics students' access into the profession, beginning with undergraduates, following the pattern of the more obviously experimental sciences like biology. The ``tetrahedral research groups'' devised at the University of Colorado, Boulder, for their successful VIGRE proposal exemplify vertical integation: each includes faculty, postdocs, graduate students and undergrads. The program is being administered with rigor. Of the twelve universities starting awards in 1999, three were not renewed: Rutgers, Carnegie-Mellon and Berkeley. How could this happen? Mackenzie quotes Calvin Moore, the Chair at Berkeley: ``One of our goals is to cultivate self-reliance. ... Some [students] thrive and others don't.'' A nice take on the program philosophy comes from Skip Garibaldi, a VIGRE-supported postdoc at UCLA whose research mentor has arranged for him to work with Jean-Piere Serre. As quoted by Mackenzie, he says: ``You can't get much above Serre, and you can't get much below me. So that's an example of vertical integration.''

A new kind of science? ``By relying on mathematical equations to describe the world, scientists for centuries have grossly limited their powers of explanation, asserts Stephen Wolfram'' is the start of Richard Monastersky's piece (Chronicle of Higher Edcation, May 17 2002) on the publication of Wolfram's long-awaited opus, "A New Kind of Science." The book is described by Jim Giles (Nature May 16 2002) as ``a call for researchers to turn away from calculus and other conventional mathematical tools ... .'' What is to replace calculus? Since John Conway's ``Game of Life'' (with roots in Von Neumann's work in the 1940s, but first brought to wide attention by Martin Gardner in the October 1970 Scientific American) we have all known that a cellular automaton can start from a couple of simple rules and generate patterns of amazing complexity. Wolfram's fundamental innovation, as best reported by Edward Rothstein (New York Times ``Arts & Ideas'' section, May 11, 2002) is to posit that such automata are actually at work behind the complex systems (turbulence, consciousness, the local structure of space-time) that currently baffle scientific inquiry. ``Not only can complex designs and processes arise from the simplest of rules, but ... simple rules actually lie beind the most sophisticated processes in the universe.'' And the corollary: some complex processes cannot be handled by scientific laws in the way we know them. ``All we can do in such cases is discover the simple rules that give birth to the complexity. ... Everything else can be found only by `experiment': the process must run its course.''

Math teachers with no math. This may only be a problem in New York, but that's unlikely. The problem is the ``alternate route'' to high school teacher certification: a teacher can become certified with a Bachelor's degree in any subject and 36 credits of college-level mathematics courses. As reported by Alfred S. Posamentier, Dean of the School of Education at City College (Op-Ed, New York Times, May 11 2002), those math courses can actually be in accounting, finance, economics or engineering. ``Mathematics is one of the most important subjects in the curriculum, a necessary foundation for many other areas of study, and we are allowing people who may know precious little about it to teach it.'' The remedy? Reinforce the State's new ``math-immersion'' route to secondary school mathematics certification: ``offer college graduates with good academic records in quantitative fields of study a special sequence of courses in the foundations of arithmetic, geometry, algebra, trigonometry, combinatorics, probability and statistics.'' And boost teacher's salaries to competitive levels.

New / old math probes the big bang. ``A reconstruction of the initial conditions of the universe by optimal mass transportation'' is the title of an article in the May 16 2002 Nature by an international team mostly based at the CNRS Observatoire de la Côte d'Azur in Nice. ``We show that, with a suitable hypothesis, the knowledge of both the present non-uniform distribution of mass and of its primordial quasi-uniform distribution uniquely determines'' a map from present positions to the respective initial ones. The mathematics they use, which they call the Monge-Ampère-Kantorovich (MAK) method, goes back in part to Monge's solution of how best to move a pile of dirt from one location to another: you construct a ``cost'' function and minimize it. They have tested the MAK reconstruction on ``data obtained by a cosmological N-body simulation with 128³ particles,'' and exhibit the results. Caution: they note that ``when working with the catalogues of several hundred thousand galaxies that are expected within a few years, a direct application of the assignment algorithm in its present state would require unresonable computational resources.''

A differential equation for organism growth. The equation is

dm
--  = a m^3/4[1-(m/M)^1/4]
dt

where m is the mass of the organism as a function of time, M is the asymptotic mass, and a is a parameter calculable from fundamental cellular properties. The equation, studied in ``Effects of size and temperature on developmental time'' by J.F. Gilhooley, E.L. Charnov, G.B.West, V.M. Savage & J.H. Brown in the May 2 2002 Nature, was previously published by West, Brown and B.J. Enquist. The parameter a is related to temperature T: it is proportional to exp(-E/kT) where k is Boltzmann's constant and E is the average energy for the biochemical reaction powering cellular metabolism. The authors deduce from these equations a general relation relating development time to body mass and temperature which they test successfully against laboratory data for fish, amphibians, aquatic insects and zooplankton (all develop at the temperature of the surrounding water) as well as bird's eggs which are incubated at much higher temperatures. The authors remark that the same equation can be used for post-embryonic growth, and that to a large extent it should be invariant across species and even taxa. If we apply it to human growth, taking a starting mass of 3 kg and an adult mass of 75 kg, and using a=0.6 (birds have a=0.65 at T=40⁰C), it predicts a mass of 69 kg at age 10, and 74 kg at age 15. A bit fast, but certainly in the right ballpark.

Trig tables in verse.

This couplet from the 5th century Arya-bhatiya (more exactly, AArya-bha.tiiya in the Velthuis transliteration described below) by the Indian astronomer Aryabhata (AAryabha.ta) contains an encoded and encapsulated sine table correct to three decimal places. The story is told by Prof. Roddam Narasimha, FRS, in a ``Words'' piece in the December 20/27 2001 Nature entitled "Sines in terse verse." The couplet transliterates as:

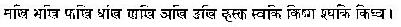
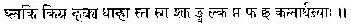
makhi bhakhi phakhi dhakhi .nakhi ~nakhi "nakhi hasjha skaki ki.sga "sghaki kighva
ghlaki kigra kakya dhaki kica sga "sjha "nva kla pta pha cha kala-ard.ha-jyaa.h

(The Nature article has an incorrect transliteration for "sghaki.) Except for the last phrase, each word encodes a number according to ``a code devised by AAryabha.ta and explained at the beginning of the book.'' This ingenious scheme was facilitated by the traditional arrangement of the Sanskrit alphabet as a 5x5 table of ``classified'' consonants, together with an equally canonical list of 8 ``unclassified" consonants and another list of vowels and diphthongs of which the first 8 (counting long and short as equivalent) are used in the code. Numerical values are assigned as follows:

 ka=1   kha=2   ga=3   gha=4  "na=5
 ca=6   cha=7   ja=8   jha=9  ~na=10
.ta=11 .tha=12 .da=13 .dha=14 .na=15
 ta=16  tha=17  da=18  dha=19  na=20
 pa=21  pha=22  ba=23  bha=24  ma=25

 ya=30  ra=40 
 la=50  va=60 
"sa=70 .sa=80 
 sa=90  ha=100

a=1 i=100 u=100² 
.r=100³ .l=100⁴ 
 e=100⁵ ai=100⁶ 
 o=100⁷ au=100⁸

The following information is necessary to translate the table into modern notation. Angles are measured in minutes of arc, and the table gives sines for multiples of 225 minutes between 0 and 5400 (a right angle). The sines are also measured in minutes (this is the reverse of radian measure!); since a length of 1 along a unit circle corresponds to 180x60/pi=3438 minutes of arc, the sines calculated from the couplet must be divided by 3438 to match modern usage. Finally, the couplet gives the differences between consecutive sines. In the following table, the running total of the AArya-bha.tiiya entries is divided by 3438 and compared with the sine given by a calculator, both rounded off to 4 decimal places.

                                        angle  sine    sine/   sine
                                         in    from    3438    from
                                       minutes verse         calculator
                                          0      0       0       0
makhi       225  khi=200 ma=25           225    225   0.0654   0.0654
bhakhi      224  khi=200 bha=24          450    449   0.1306   0.1305
phakhi      222  khi=200 pha=22          675    671   0.1952   0.1951
dhakhi      219  khi=200 dha=19          900    890   0.2589   0.2588
.nakhi      215  khi=200 .na=15         1125   1105   0.3214   0.3214
~nakhi      210  khi=200 ~na=10         1350   1315   0.3825   0.3827
"nakhi      205  khi=200 "na=5          1575   1520   0.4421   0.4423 
hasjha      199  ha=100 sa=90 jha=9     1800   1719   0.5      0.5
skaki       191  ki=100 sa=90 ka=1      2025   1910   0.5556   0.5556
ki.sga      183  ki=100 .sa=80 ga=3     2250   2093   0.6088   0.6088
"sghaki     174  ki=100 "sa=70 gha=4    2425   2267   0.6594   0.6593
kighva      164  ki=100 va=60 gha=4     2700   2431   0.7071   0.7071
ghlaki      154  ki=100 gha=4 la=50     2925   2585   0.7519   0.7518 
kigra       143  ki=100 ra=40 ga=3      3150   2728   0.7935   0.7934
hakya       131  ha=100 ya=30 ka=1      3375   2859   0.8316   0.8315
dhaki       119  dha=19 ki=ka+i=100     3600   2978   0.8662   0.8660
kica        106  ka=1 i=100 ca=6        3825   3084   0.8970   0.8969
sga          93  sa=90 ga=3             4050   3177   0.9241   0.9239
"sjha        79  "sa=70 jha=9           4275   3256   0.9471   0.9469
"nva         65  "na=5 va=60            4500   3321   0.9660   0.9659
kla          51  ka=1 la=50             4725   3372   0.9808   0.9808
pta          37  pa=21 ta=16            4950   3409   0.9916   0.9914
pha          22                         5175   3431   0.9980   0.9979
cha           7                         5400   3438   1.       1.

-Tony Phillips
Stony Brook

Math in the Media Archive