February 2001
 |
| Plimpton 322, George A. Plimpton Collection, Rare Book and Manuscript Library, Columbia University. Click for larger image. |
Rereading Plimpton 322. Plimpton 322, the tiny dark star of
Columbia University's Rare Book Library, is probably the world's best
known piece of Mesopotamian mathematics. A
clay tablet, about 5 inches long and 3.5 inches wide,
with 4 columns and 15 rows
of cuneiform hexadecimal numbers, it is usually dated 1900-1600 BC.
Sir Christopher Zeeman lectured on it in San Antonio in 1995 AD,
calls it ``the oldest preserved document on number theory," and gives
a mathematical argument for its interpretation as a set of
pythagorean triples. Lectures
avilable online.
The January 27 2001 Science News has a piece by Ian Porteous
describing a recent reevaluation of the mathematical content of the
tablet. The work is due to Eleanor Robson (Oriental Institute, Oxford)
and is presented as an example of ``new scholarly
approaches to Mesopotamian mathematics" which ``combine historical,
linguistic and mathematical techniques." Dr Robson pins down the
date of the tablet to 1800 +/- 40 BC, and gives an alternative
explanation of the tablet's purpose: it ``served as a guide for a
teacher preparing exercises involving squares and reciprocals."
Despite this downgrading from number theory to arithmetic, Robson
considers Plimpton 322
``the epitome of Mesopotamian mathematical culture at its best. ... It's a
well-organized, well-executed, beautiful piece of mathematics."
``Loving Math Infinitely" is the title of a piece by
Josephina Alvarez, professor of mathematics at New Mexico
State University at Las Cruces, that ran in the Chronicle Review section
of the January 19, 2001
Chronicle of Higher Education.
Prof. Alvarez describes her experiences teaching ``a course on
mathematics appreciation for nonscience majors." This is a rich
piece, with many valuable ideas for mathematics teachers at any
level. She finds that in order to reach her students, she has to
``look into their training and
interests. I need to learn to use their language. My challenge
is to extract the mathematical ideas in music, philosophy,
art, and other seemingly nonmathematical fields." She elaborates
on ``As soon as I knew what I should be looking for, I started to
see mathematics in unexpected places." with many examples, and
concludes: ``Interestingly enough, once we saw mathematics as firmly rooted
in human need and experience, it seemed easy to depart on a
tour of increasing abstraction." To summarize her article in
two sentences: ``Mathematics appreciation is more than a course. It is an
attitude that we should cultivate in every mathematics course."
How do fish swim? ``The dynamics of swimming fish and
flapping flags involves a complicated interaction
of their deformable shapes with the surrounding fluid flow." This is
the beginning of a ``letter to Nature" (14 December 2000) from
a Courant Institute/Rockefeller University team headed by Jun Zhang.
Their research used flexible filaments in a flowing soap film 3-4
microns thick.
In particular they report that beyond
a certain critical length the system becomes bi-stable, with both
a
``stretched-straight state" and a ``stable flapping state" possible.
|
| A snapshot of the flapping state. Note that the end of the filament is near the center of the image. Image from NYU Wetlab, used with permission. Click for larger image. |
.
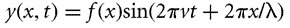Here, y(x, t) is the horizontal displacement of the filament from
the centre-line,
measured at a vertical distance x from the fixed point for time t.
f(x) is a spatial
envelope function (increasing monotonically from the fixed point),
nu is the flapping frequency and lambda the wavelength."
An interesting final point: ``Swimming offers alternatives comparable to the bistability of our filament. The stretched-straight state is the analogue of a glide, whereas the flapping state is analogous to swimming. Efficient propulsion uses the natural oscillations of the swimmer, which in the filament is a property mediated by stiffness." A web presentation of this research is available.
Digital Archimedes. The thousand-year-old
palimpsest
that turned up on the front pages in 1998 is undergoing a thoroughly
modern analysis. A report entitled ``Through the Layers, a Glimmer of
Archimedes" by Lawrence Biemiller (The Chronicle of Higher Education,
January 26, 2001) describes this treasure: a precious euchologion,
a 10th century Greek prayer book, was written on parchment that had
previously been used for a collection of works by the great Archimedes.
Even though the pages had been scraped clear of the original text, enough
remained for the Danish scholar Johan Ludvig Heiberg to recognize. The
discovery (published in 1907) was sensational: among other works the
manuscript contained a copy of ``The Method," an important work of
Archimedes that had been thought completely lost. Biemiller tells
the story of how this item came to be sold at Christies' in 1998
(for $2 million) and how the present owner has agreed to pay for
the Walters Art Gallery in Baltimore to take over the conservation of
the manuscript and the computer-aided digital imaging of its
pages. Two teams, one from
Johns Hopkins and one from the Rochester Institute
of Technology, are collaborating with the Walters. They predict a
much more complete transcription of the text and, quite important,
access to the original drawings. The project should take four years.
Math teachers are nerds ... not. John Dunford, a math
teacher himself (and general secretary of the somewhat ominously named
Secondary Heads Association) takes issue with a survey of 12-year-old
schoolchildren's ``impressions of their maths teachers." In a piece in
the January 4, 2001 Guardian he defends the profession from the
merciless gaze of the young: ``Fat, bald nerds with glasses and beards
apparently predominate at the front of maths classrooms. These sad
figures are apparently seen as unmarried and unstylish, wrinkled from
all the hard thinking that they have had to do in order to solve maths
problems throughout their lives." Not so, says Dunford. Speaking of his
colleagues over the years: ``I cannot really recall anyone who might have
been described as a nerd. ... family people mostly, with a good range of
interests from swimming and badminton to reading and cooking." But wait!
``There could be an age factor too. I may not find my colleagues nerdish,
but I do recall my own maths teachers at school as coming into that
category."
The piece is available online.
Math and Fiction. Incompatible careers? Not if you
ask Manil Suri, expert in partial differential
equations, Professor of Mathematics at the University of
Maryland Baltimore County,
and author of a New Yorker short
story (``The Seven Circles," February 14, 2000) and a novel
``The Death of Vishnu" (Norton, January 2001). Suri was interviewed by
Ivar Stakgold in the January-February 2001 SIAM News.
The interview ranges over many topics, but keeps returning to
the similarities and differences between doing math and writing
fiction. Suri: ``What's a little eerie is how similar the thought
processes can be for the two activities. Suppose I am trying to
decide whether a mathematical entity X is bounded.
I might try to think of varous ways that X might try
to misbehave ... . Fiction presents a similar scenario -- perhaps
X is now a character in a certain situation. To find out
what happens next, I would try to put myself in X's place,
looking for all the ways I could proceed, maneuvering around any
of the story's imposed constraints, and choosing the most
interesting path." He mentions a reading at MSRI after which a
colleague told him ``It's all about Fourier series," i.e. that
``all fiction is composed of the same Fourier modes: love, death,
marriage, sex and so on, and one gets different stories by
assembling different combinations of these basis functions."
Prof. Suri knows how to milk a metaphor: ``Certainly a key
strategy to getting fiction published is to orthogonalize to what
has been written before."
-Tony Phillips
Stony Brook