``Brain's Math Machine Traced to 2 Circuits.'' This was the New York Times' take (Sandra Blakeslee, May 11) on a report in the May 7 Science by S. Dehaene, E. Spelke, P. Pinel, R. Stanescu and S.Tsivkin.

The report, ``Sources of Mathematical Thinking: Behavioral and Brain-Imaging Evidence,'' demonstrates that there are at least two different loci in the brain involved in arithmetic, and that the two loci do different things.

• Exact calculation is accompanied by a ``large and strictly left-lateralized activation in the left inferior frontal lobe.''

• Approximate calculation tasks activate a region in the bilateral inferior parietal lobule.

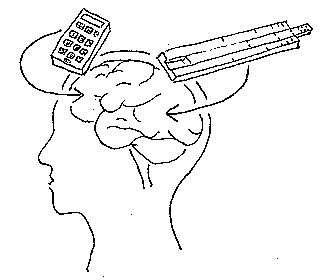
The mathematical mind: exact calculation locus in the
left inferior frontal lobe, approximate calculation
locus in the bilateral inferior parietal lobule.

These two loci are also associated with other mental activities:

• The left inferior frontal lobe is also activated during verbal association tasks; the behavioral aspect of this research, a set of experiments with bilingual subjects, shows that in fact exact calculation is language-linked, whereas approximate calculation is not.

• The authors remark that bilateral inferior parietal loci are also activated during visually guided hand and eye movements and mental rotation. In an essay in the same issue of Science, Brian Butterworth points out that the proximity of the areas that control finger movements and approximate calculations ``raises the possibility that these brain regions contribute to finger counting and finger calculation ... and prompts the suspicion that the parietal lobes, in the course of development and learning, come to support the digital representation of numbers.'' Presumably this refers to a pre-verbal ideation of number, with the first three fingers coming to represent the equivalence class 3, etc.

• ``Symbolic arithmetic is a cultural invention specific to humans, and its development depended on the progressive improvement of number notation systems.'' i.e. of mathematical language.

• ``Approximate arithmetic, in contrast, shows no dependence on language ... An interesting, though clearly speculative, possibility is that this language-independent representation of numerical quantity is related to the preverbal numerical abilities that have been independently established in various animal species and in human infants.''

• ``Together, these results may indicate that the human sense of numerical quantities has a long evolutionary history, a distinct developmental trajectory, and a dedicated cerebral substrate. In educated humans, it could provide the foundation for an integration with language-based representations of numbers. Much of advanced mathematics may build on this integration.''

Multiple Intelligences. From the point of view of teaching and learning mathematics, it is interesting to situate this research in the context of ``multiple intelligences.'' This is a circle of ideas developed by Howard Gardner in a series of books starting with Frames of Mind : The Theory of Multiple Intelligences in 1983. (Gardner also is featured in an Edge piece: Truth, Beauty, and Goodness: Education for All Human Beings: A Talk With Howard Gardner.) His classification is based on an empirical effort to understand all human mental abilities. The seven intelligences he proposed:

spatial, linguistic, logical-mathematical, musical, intrapersonal, interpersonal, bodily-kinesthetic

are each ``a capacity, with its component processes, that is geared to a specific content in the world (such as musical sounds or spatial patterns)''. This quote is from his Reflections on Multiple Intelligences: Myths and Messages, where he also mentions that ten years later he proposes adding to the list an eighth intelligence, that

of the naturalist.

The experimental results of Deheane, Spelke and their collaborators strongly suggest that mathematical ability must involve at least three of Gardner's intelligences: the logical-mathematical (by definition) the spatial and the linguistic.

The concept of multiple mathematical intelligences was put forth, almost at the same time, in a work called Math for Smarty Pants by Marilyn Burns (Little, Brown & Co., 1982). She remarks: ``being smart in math can mean several things, and different things.''

``There are some kids who are whizzes at dealing with numbers. They do arithmetic fast, really fast. ...'' ``Then there are the kids who are great with shapes, who can `see' things easily in their heads. ...'' ``Some kids are good at strategy games and puzzles that don't have much to do with either arithmetic or shape, but have more to do with thinking logically to figure things out. ...''

When I came across Burns' book I was very pleased to see explicitly written out, for the first time, what I had felt as a mathematician for many years: there are different kinds of mathematical minds. Besides helping me make sense of a career spent in departments with logicians, analysts and algebraists it made me very receptive to the ``rule of three'' as propounded by the members of the Harvard Calculus Consortium, which has become the Rule of Four in the second edition of their Calculus: ``Where appropriate, topics should be presented geometrically, numerically, analytically and verbally.'' It makes sense to access as many intelligences as are available.

and Multiple Mathematical Personalities? One aspect of the phenomenon that neither Gardner nor the Dehaene-Spelke team seem to have gone into is the correlation between the various intelligences and personality traits. In a department of research mathematicians where the mathematical intelligences, at least, can be assumed to be present in their most extreme form, there is considerable evidence of a correlation, which may not be noticeable in the general population, with various personality types. Without going into too many specifics, let me tell the story of a mathematician, a male, who changed fields early in his career. When his wife was asked at a cocktail party what her husband did (this probably dates the story) she said: ``He's a logician.'' ``But,'' she quickly added, ``he used to be a topologist.''

--Tony Phillips

 
Comments: webmaster@ams.org
© copyright 1999, American Mathematical Society.