 . We can measure the quality
of these approximations by noticing that
. We can measure the quality
of these approximations by noticing that  - rk < 1/10k : the
error is less than one over the denominator of the fraction.
- rk < 1/10k : the
error is less than one over the denominator of the fraction.
 = 3.14159... the rational numbers
= 3.14159... the rational numbers
| r0 = 3, |
| r1 = 3.1 = 31/10, |
| r2 = 3.14 = 314/1000, |
| r3 = 3.141 = 3141/10000, |
| ... |
give a sequence of
better and better approximations to  . We can measure the quality
of these approximations by noticing that
. We can measure the quality
of these approximations by noticing that  - rk < 1/10k : the
error is less than one over the denominator of the fraction.
- rk < 1/10k : the
error is less than one over the denominator of the fraction.
Similarly 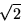 = 1.41421... can be apprroximated by the
sequence of rational numbers
= 1.41421... can be apprroximated by the
sequence of rational numbers
| 1, |
| 14/10, |
| 141/1000, |
| 1414/10000, |
| ... |
with the same accuracy as the
approximations to  .
.
When we allow other denominators than powers of 10, the
picture becomes different. For example
22/7 is a well known rational approximation to  . The error in the
approximation is 0.00126. Another rational approximation to
. The error in the
approximation is 0.00126. Another rational approximation to
 is 355/113; this time the error is 0.000000266.
is 355/113; this time the error is 0.000000266.
The best rational approximation to 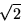 with a denominator less than 10
is 7/5; the error is .0142. The best with a denominator less than 200
is 239/169, with error .0000124. This is much less satisfactory
than the rational approximations to
with a denominator less than 10
is 7/5; the error is .0142. The best with a denominator less than 200
is 239/169, with error .0000124. This is much less satisfactory
than the rational approximations to  .
.
Observations like these have led mathematicians to set up a hierarchy among irrational numbers, according to how difficult they are to approximate with rationals. It is in this sense that one irrational is more irrational than another. To make the criterion precise, we start from the following fact:
Hurwitz' Theorem: Every number has infinitely many rational approximations p/q, where the approximation p/q has error less than 1/q2.
The criterion can then be stated in terms of: how much less
than 1/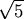 q2?
to compare
q2?
to compare  and
and 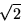 in this regard, some of the best
rational approximations can be displayed in a table. Here
we will reckon the error E in terms of Hurwitz' bound
M = 1/
in this regard, some of the best
rational approximations can be displayed in a table. Here
we will reckon the error E in terms of Hurwitz' bound
M = 1/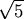 q2
by tabulating the quotient E/M.
q2
by tabulating the quotient E/M.
 : : | p/q | E = error | M = 1/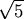 q2 q2 | E/M |
| 22/7 | .00126 | .0091 | 0.13 | |
| 355/113 | .000000266 | .0000350 | 0.007 | |
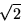 : : | p/q | E = error | M = 1/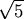 q2 q2 | E/M |
| 7/5 | .0142 | .0179 | 0.79 | |
| 239/169 | .0000124 | .0000156 | 0.79 |
These tables suggest that  admits much better rational approximations than
admits much better rational approximations than 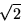 .
In fact no rational approximation to
.
In fact no rational approximation to 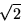 ever
gets an E/M ratio as small as .13, let alone .007, and
ever
gets an E/M ratio as small as .13, let alone .007, and 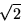 is
really harder to approximate with rationals than
is
really harder to approximate with rationals than  . In
this precise sense
. In
this precise sense 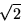 is a more irrational number
than
is a more irrational number
than  .
.
Corrected 11/12/13
Back to first irrational page.
|
© copyright 1999, American Mathematical Society. |