
Gravitational Lens
Galaxy Cluster 0024+1654
W.N. Colley (Princeton University), E. Turner (Princeton University)
J.A. Tyson (AT&T Bell Labs) and NASA

Grawitacyjne soczewkowaniai geometryczne soczewkowania (this page in Polish)
This page in Hindi
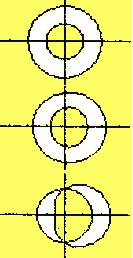
A recent New York Times article (John Noble Wilford, "The Universe as Telescope", 12/29/98) gave news of progress in the study of gravitational lensing. This phenomenon, predicted by Einstein, is caused by the deflection of light rays by massive objects. The article displayed this image.

Gravitational Lens
Galaxy Cluster 0024+1654
W.N. Colley (Princeton University), E. Turner (Princeton University)
J.A. Tyson (AT&T Bell Labs) and NASA
See: Gravitational Lens Captures Image of Primeval Galaxy on the AURA Hubble Space Telescope Public Pictures Website. Here is the beginning of the caption at that site: "This Hubble Space Telescope image shows several blue, loop-shaped objects that actually are multiple images of the same galaxy. They have been duplicated by the gravitational lens of the cluster of yellow, elliptical and spiral galaxies - called 0024+1654 - near the photograph's center. The gravitational lens is produced by the cluster's tremendous gravitational field that bends light to magnify, brighten and distort the image of a more distant object. How distorted the image becomes and how many copies are made depends on the alignment between the foreground cluster and the more distant galaxy, which is behind the cluster." (Image and text reproduced with permission of AURA/STScI.)
The bending of light rays may seem curious and even paradoxical to people who are used to thinking that light rays travel in straight lines. But what is actually happening is stranger still: a massive object deforms the nearby geometry of space, so that instead of flat it becomes curved. The light rays are still going as straight as they can, but in a curved region of space going as straight as you can may entail bending. We have an example right here on the surface of the Earth, where the straightest possible routes from one point to another lie along great circles.
Besides the surface of the Earth, there are other familiar spaces which show intrinsic curvature: cones. A cone has a curvature singularity at its apex; in fact this feature makes it an appropriate first step in creating a simple geometrical analogue of the space distortion caused by a small, massive object. The pointiness of the cone is the analogue of the mass. The geometry of the cone, and its generalization to three-dimensional cones, manifest geometric lensing effects which can be worked out by hand and which give a reasonable first approximation to those produced by gravity. These images should be compared with those in Einstein Rings from Gravitational Lensing (by Peter Newbury of the University of British Columbia), which were produced by ray-tracing: following light paths in the metric given by the solution of Einstein's equations in the neighborhood of a spherically symmetric mass.
TWO-DIMENSIONAL CONES. A cone for ice cream or even better a conical paper cup is good for getting an idea of what the intrinsic curvature of space can be. Imagine two-dimensional creatures living in a two-dimensional universe which includes the surface of the paper cup. Imagine that this paper cup is very big and that the cone point is very far away. Then they might well feel they were living in a flat world. If the cone is slit along a line passing through the cone point, what is left looks like a pie minus a slice and can be flattened out perfectly with no creasing or crinkling. The inhabitants would not notice any change at all. Light rays traveling in this two-dimensional universe (avoiding the cone point, of course) also cannot tell that they are not traveling in a flat plane. So we can trace one of their paths on the cone by slitting, flattening, drawing part of a straight line, and reassembling the cone. It may take several slittings to complete a path. (Another method is to lay a strip of Scotch tape on the surface. The tape, if laid flat, must follow the same path a light ray would take.)


The path of a light ray on the cone.
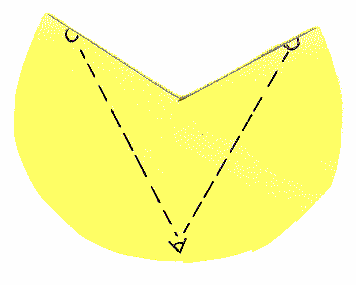
The light rays from the two halves appear to the observer as
emanating from two objects.
The image consists of two regions in the observer's one-dimensional
visual field.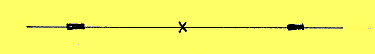
THREE-DIMENSIONAL CONES. A 3-dimensional cone is harder to think about because we can only see it ``from the outside" in four-dimensional space (just as the 2-dimensional cone can only be seen ``from the outside" in three dimensions). The fourth dimension here is an aid to maintaining the analogy with surface phenomena. In terms of our 3-dimensional universe it does not necessarily have any physical reality!
Just as the paper cone has a circle as its base, the simplest 3-dimensional cone has a 2-dimensional spherical surface as its base. We will consider a ``right" cone in which each point of the surface is the same distance from the cone point.
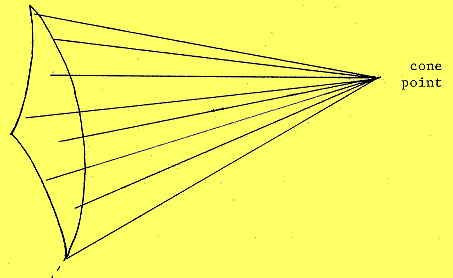
This figure represents the piece of the cone corresponding to a triangle on the spherical surface. The entire cone cannot be drawn this way.
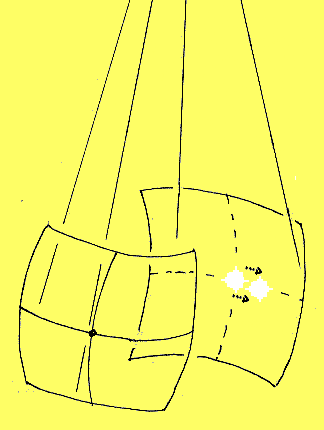
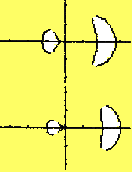
GEOMETRIC LENSING IN A THREE-DIMENSIONAL CONE. If the object is centered on the cone line through the South Pole, then for each great circle there will be two linear images, equidistant from the image of the singularity, and these will combine to form a halo about the singularity in the observer's visual field.
|
  |
|---|
As the object moves away from the cone line through the South Pole, the halo will will disassociate into two separate images. If the motion continues, one of these images will disappear "behind the singularity," just as in the 2-dimensional case.
For a large selection of web resources on general relativity, see Relativity on the Web, a page maintained by Chris Hillman of the University of Washington.
--Tony Phillips