A calculator exercise:
The Effect of the Sun on the Tides in Long Island Sound


The sun is about 370 times as far away as the moon. But the sun is also about 370 times as wide as the moon. The near-concidence of these factors implies that the solar tide should be comparable in strength to the lunar. In fact it is weaker, but it is strong enough to affect the times and the heights of the tides.

In this exercise, we will calculate how the sun affects the tides at four different days during the first half of the month. (We start our month at a new moon, when the sun and moon are lined up and on the same side of the earth). For simplicity we will consider only the fundamental lunar and solar constituents, M2 and S2, and compare the times of high tides (relative maxima) of the M2 function (moon alone) and the M2+S2 (sun and moon together), using tide data (from Brown and Park) for the Stony Brook Yacht Club.

The sum M2 + S2 is the tide we would have if the earth's and moon's orbits were circular and in the same plane, and if the axis of the earth's rotation were perpendicular to that plane.

The S2 constituent has speed 30 degrees/hour, corresponding to twice the apparent angular speed of the sun across the sky. ``Twice" because the sun, like the moon, produces two diametrically opposite bulges of water on the earth's surface. (You can understand it this way: When the sun is high in the sky here it is pulling the water away from the earth; at the same time, at our antipodal point, it is pulling the earth away from the water.) A speed of 30 degrees/hour corresponds to two complete oscillations per day (30x24 = 2x360). That is what the word ``semidiurnal" refers to. The amplitude of the S2 constituent at the Stony Brook Yacht Club has been measured to be .51 feet.

The moon's apparent angular speed across the sky is less than that of the sun, because it is traveling around the earth (once in about 28 days) in the same direction as the rotation of the earth. Combining these two motions gives the M2 constituent a speed of 28.984 degrees/hour. (You can calculate that this makes today's M2 high tides 50.46 minutes later than yesterday's.) The M2 amplitude at the SBYC has been measured to be 2.59 feet.

So the two functions we want to compare are:

M2: 2.59 cos(28.984 t)

which would be the tide from the moon alone, and

M2+ S2: 2.59 cos(28.984 t) + .51 cos(30 t)

the combined solar and lunar tide. Remember to set your calculator in degrees for this calculation!

The high tides are the local maxima of the tidal height function. In these exercises we will use calculus to compare M2 and M2 + S2, to understand how the sun changes the times and the heights of the high tides.

Exercise 1. Calculate the times and the heights of the M2 and M2 + S2 high tides on day 0 (t=0..24). You should find a couple of minutes difference in time, and the M2 + S2 tide .5 feet higher than M2 alone. The stronger tides caused by the the sun and the moon working together are called SPRING TIDES.

Spring Tides: on day 0 (and day 14) the solar and lunar bulges add to give the highest tides of the month.


Exercise 2. Do the same for day 3 (t=72..96). You should find that the two tides are almost the same height, but that the M2 + S2 high tides come about 22 minutes earlier. This is called the PRIMING of the tide, and occurs during the first week after the new moon (and during the first week after the full moon).

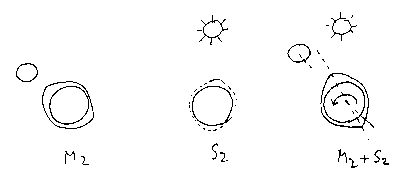Priming: on day 3 (and 17) the solar bulge is about 45 degrees behind the lunar. This makes the high tide come some 20 minutes earlier. The circular arrow shows the direction of the earth's rotation.


Exercise 3. Do the same for day 7 (t=168..192). You should find a very small difference in time, but the M2 + S2 tide about .5 feet lower than the M2. The weaker tides caused by the sun and the moon working at cross purposes are called NEAP TIDES.

Neap tides: on day 7 (and day 21) the solar and lunar bulges are 90 degres out of phase. The lunar maximum matches the solar minimum, and the tides subtract.


Exercise 4. Do the same for day 10 (t=240..264). You should find that the two tides are almost the same height, but that the M2 + S2 high tides come about 20 minutes later. This is called the LAGGING of the tide, and occurs during the second week after the new moon (and during the second week after the full moon).

Lagging: on day 10 (and 24) the antipodal solar bulge is about 45 degrees ahead of the lunar bulge. This makes the high tide come some 20 minutes later.


Click here to check your answers against mine.

Remember to set your calculator back to radians when you are finished!

Back to Main Tide page.

Back to Tony's Home Page.