Homework. Due March 16.

We saw last time that the ``checkerboard'' problem was not in fact a pigeonhole problem: Since 2 white squares were removed, the board had 2 more white squares than black squares; since each domino covers one white square and one black square, there is no way for dominos to cover all the remaining squares.

1. Suppose that the board has shape 2n X 2k, for any positive integers n and k. Show that the result is the same as for the 8 X 8 board. What happens if the board has one even side and one odd? If both sides are odd? This problem depends on parity. Can you state it in general in the form: the board with 2 opposite corners missing can be covered by dominos iff and only if N is odd? For some number N associated with the problem.

2. The numbers 1 through 10 are written in a row. Can the signs "+" and "-" be placed between them in such a way that the resulting expression adds up to 0?

3. If n is a positive integer such that 2n+1 is a perfect square show that n+1 is the sum of two successive perfect squares.

4. Twenty-five men and twenty-five women are seated at a round table. Show that there must be at least one person at the table who is seated between two men.

5. Below is a picture of the town of Königsberg, Prussia (now Kaliningrad, Russia). When the Swiss mathematician Leonhard Euler (1707-1783) traveled there, there were seven bridges connecting the central island, and the sides of the rivers, as shown. Euler wondered if it would be possible for a person to walk through the city in such a way as to cross each of the seven bridges exactly once.
   

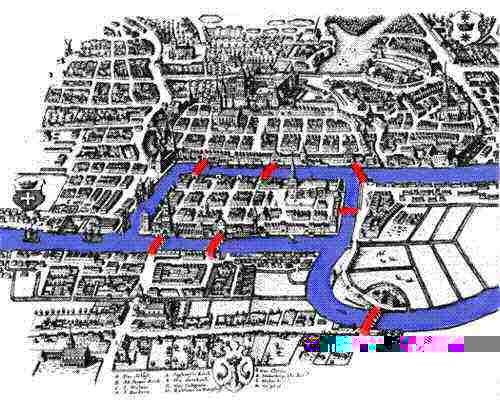
   Is this possible?
   Suppose that the top left bridge in the picture is closed. Now is it possible?
   Can you state a general principle manifested here?