A basic question is whether or not there is a hyperbolic metric on $S$ such that the configuration is isotopic to a collection of closed geodesics intersecting transversally. We will say in this case that the configuration can be realized by geodesics. It is an old but remarkable fact that the following simple configuration on the pair of pants cannot be realized by a geodesic in any metric of negative curvature.
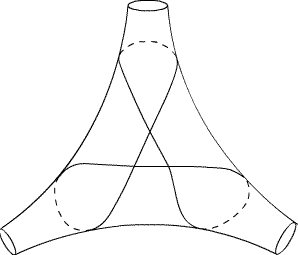
Fig. 1. This example was discovered and published in 1999 by Joel Hass and Peter Scott [HS]. As they remark, their proof of non-realizability can be by replaced by an argument, due to Ian Agol, using the Gauss-Bonnet Theorem.
In this paper Agol's argument is generalized to produce an infinite family of non-realizable configurations, the polygonal impossible configurations, including a unicursal, non-realizable configuration filling the surface of genus $n$ with $k$ punctures for every $n\geq 2$ and $k\geq 0$. In some sense polygonal impossible configurations are all of the non-realizable examples that can be constructed using this general form of the argument.
Preliminaries: We will construct configurations with the following properties.Proof: Set $n_i$ to be the number of vertices of $A_i$, and $\alpha_{i,j}$, $j=1,\dots, n_i$ to be the interior angle at the $j$th vertex of $A_i$. Likewise set $m_i$ to be the number of vertices of $B_i$, and $\beta_{i,j}$, $j=1,\dots, m_i$ to be the interior angle at the $j$th vertex of $B_i$. Assume all the edges are geodesic arcs extending smoothly from polygon to polygon, so that each of the $\alpha_{i,j}$ is complementary to exactly two of the $\beta_{i,j}$. The Gauss-Bonnet theorem [Wu] gives $$\alpha_{1,1} + \alpha_{1,2} + \cdots \alpha_{1,n_1} < (n_1-2)\pi\\ \\\dots\\ \alpha_{p,1} +\alpha_{p,2} + \cdots \alpha_{p,n_p} < (n_p-2)\pi.$$ Adding these equations, $$\sum _{i=1}^p\sum_{j=1}^{n_i}\alpha_{i,j}< (N - 2p)\pi. ~~~~ (*)$$ Similarly, the sum of all the $\beta$s is strictly less than $(2N - 2q)\pi$. On the other hand each $\beta$ is $\pi - \alpha$ for some $\alpha$, with each $\alpha$ occurring exactly twice. So $$(2N-2q)\pi > \sum _{i=1}^q\sum_{j=1}^{m_i}\beta_{i,j} = 2\sum _{i=1}^p\sum_{j=1}^{n_i}(\pi -\alpha_{i,j}) = 2N\pi -2\sum _{i=1}^p\sum_{j=1}^{n_i}\alpha_{i,j}$$ i.e. $\sum _{i=1}^p\sum_{j=1}^{n_i}\alpha_{i,j} > q\pi$. Since by the construction $q=N-2p$, this inequality contradicts $(*)$.
We will call a polygonal configuration on a smooth surface minimal if it fills the surface, and has the smallest possible number of vertices. Since $r\geq 1$, $(*)$ implies that $p$, the number of $A$-polygons, must satisfy $p\geq 2g-1$. And since each $A$-polygon is at least a triangle, the minimum number of vertices for a polygonal impossible configuration filling the smooth surface of genus $g \geq 2$ is $6g-3$.
The smallest possible $N$ is $N=3$. Here $p$ and $q$ must equal 1, with $A_1$ a triangle and $B_1$ a hexagon. There are two ways to make the identification, with different results, as shown in Fig. 2.
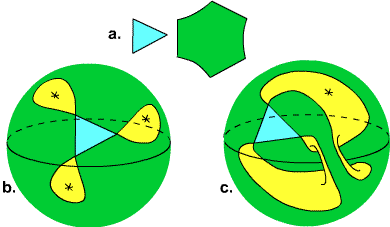
Fig. 2. $N=3$. a. one triangle, one hexagon. b. (Asterisks represent punctures). This is the configuration exhibited by Hass and Scott; the identification gives $r=3$ and $g_{\mathcal{P}}=0$, yielding a (1-track) impossible configuration on the 3-punctured sphere. c. Otherwise the identification gives $r=1$ and $g_{\mathcal{P}}=1$; hence a graph on the torus which becomes an impossible (3-track) configuration on the punctured torus.
Proposition 2. There exists a minimal unicursal impossible polygonal configuration filling the smooth surface of genus $n$.
Proof:We begin with genus $2$.
Fig. 3. A 1-track impossible configuration on the genus-2 surface with $N=9, p=3, q=3$ (decagon and 2 squares), $r=1$.
This construction can be extended to give an impossible configuration $\mathcal{P}_n$ filling the surface of genus $n$, for each $n\geq 2$.
Fig. 4. The configuration $\mathcal{P}_n$ has $p=2n-1$ triangles corner-matched by $2n-2$ squares and a $(4n+2)$-gon. It has $r=1$ (see Fig. 5) and therefore genus $n$.
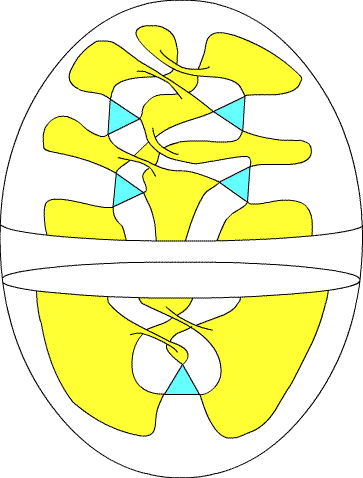
Fig. 5. The boundary of $\mathcal{P}_n$ is a polygon with $6n-3$ vertices. For this picture the $B$-polygons have been suppressed.
Assertion: The configuration $\mathcal{P}_n$ has a single track if $n\equiv 0$ or 2 mod 3, and 3 tracks if $n\equiv 1$ mod 3.
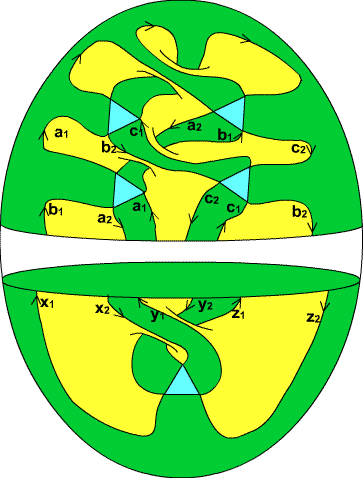
Fig. 6. The top and the bottom of $\mathcal{P}_n$, with arrows tracing a path through the configuration.
In fact, at each stage in the assembly there are 3 tracks of the curve, ${\bf a_1}{\bf a_2},{\bf b_1}{\bf b_2}$ and ${\bf c_1}{\bf c_2}$. Adding the next stage permutes the six free ends by the cycle $({\bf a_1}{\bf b_1}{\bf c_1})({\bf a_2}{\bf c_2}{\bf b_2})$. After 0 iterations ($n=2$), the ends ${\bf a_1},{\bf b_2},{\bf c_1},{\bf a_2},{\bf b_1},{\bf c_2}$ will be joined respectively to the free ends of the bottom ${\bf x_1},{\bf x_2},{\bf y_1},{\bf y_2},{\bf z_1},{\bf z_2}$ resulting in a single loop: ${\bf x_1}{\bf a_1}{\bf a_2}{\bf y_2}{\bf y_1}{\bf c_1} {\bf c_2}{\bf z_2}{\bf z_1}{\bf b_1}{\bf b_2}{\bf x_2}$. After 1 iteration ($n=3$), there still is a single loop: ${\bf x_1}{\bf b_1}{\bf b_2}{\bf z_2}{\bf z_1}{\bf c_1} {\bf c_2}{\bf y_2}{\bf y_1}{\bf a_1}{\bf a_2}{\bf x_2}$. But after 2 iterations ($n=4$) the identifications give three loops: ${\bf x_1}{\bf c_1}{\bf c_2}{\bf x_2}$, ${\bf y_1}{\bf b_1} {\bf b_2}{\bf y_2}$, ${\bf z_1}{\bf a_1}{\bf a_2}{\bf z_2}$. Since the permutation has order 3, the sequence repeats.
The case of genus $3k+4$, and $k\geq 0$ requires a slightly more complicated construction to produce a family of minimal, unicursal, filling configurations.
Fig. 7. The configuration $\mathcal{Q}_k$ has $6k+7$ $A$-polygons, all triangles, so $N=18k+21$ and $q=6k+7$. The $B$-polygons are $6k+6$ squares and one $12k+18$-gon. One can check this configuration is unicursal and that $r=1$, so the genus is $\frac{1}{2}(2+p-r)=3k+4$ and the configuration is filling.
This theorem is proved in the Appendix.
For configurations filling surfaces with two or more punctures, this theorem produces a conflict between being unicursal and being minimal, as defined above. Suppose that $\mathcal{P}$ $(N, p, q, r)$ is a minimal, unicursal configuration on the smooth surface $\Sigma_{n,0}$ of genus $n$. By minimality and $(*)$, $p=2n-1$. Since $r=1$ the surface can be given one puncture in that complementary region; the result will be a minimal, unicursal configuration filling $\Sigma_{n,1}$. No problem so far. Working on $\Sigma_{n,2}$ we will need $r=2$ and, by $(*)$, $p=2n$. Minimality would require all $p$ of the $A$-polygons to be triangles, but then $N=3p$ would be even and, by Theorem 1, the configuration cannot be unicursal. Both possibilities can be realized separately, by adding to the configutation $\mathcal{P}$ one or the other of the sub-configurations shown in Fig. 8.
Fig. 8. These two sub-configuration can be added to a configuration $\mathcal{P}$ filling $\Sigma_{n,k}$. Sub-configuration a. can be interpolated along a free edge of any $B$-polygon; b. can be inserted at any of the interfaces between a $B$-polygon and an $A$. The result is a configuration on the same surface, but with $r$ increased by 1. Puncturing the new $C$-cell will give a polygonal impossible configuration filling $\Sigma_{n,k+1}$. If $\mathcal{P}$ was minimal, using a. will also give a minimal configuration; but it will clearly not be unicursal. If $\mathcal{P}$ was unicursal, using b. will also give a unicursal configuration; but it will not be minimal.
This discussion can be summarized as follows:
Proposition 3. There exist a minimal polygonal impossible configuration and a unicursal polygonal impossible configuration filling the surface of genus $n$ with $k$ punctures, $n\geq 2, k\geq 0$. These are generally different.
The examples shown in Figs. 2 and 3 suggest the following statements.
Theorem 1. The number of tracks of a polygonal impossible configuration is congruent mod 2 to the number of vertices. In particular, such a configuration can only be unicursal if the number of vertices is odd.Theorem 2. A polygonal impossible configuration with an odd number of vertices can be adjusted, by changing the identifications in step 4 of the algorithm, to be unicursal. (This may change the genus; see Remark below.)
Preliminaries for the proofs.
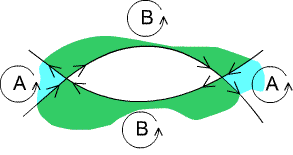
Fig. 9. The $A$ and $B$ orientations are adjusted to give a well-defined orientation on each track.
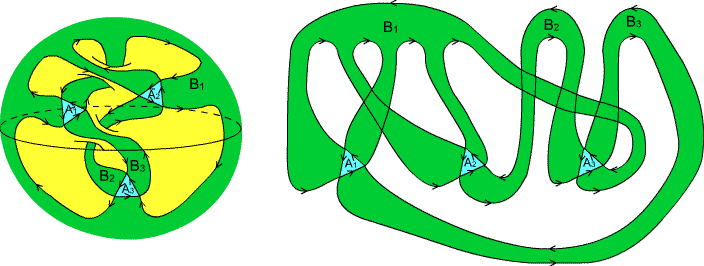
Fig. 10. The projection of a polygonal impossible configuration can be displayed with all the $B$ polygons at the top, all the $A$ polygons at the bottom, and so that the only horizontal tangents appear at the top and at the bottom. This figure shows the configuration from Fig. 3, oriented as above, with its display in this form.
1. We show that the sum of the rotation numbers of the projected
complex of curves
is even. This is the sum of the degrees of the Gauss maps, which take a
parameter value to the unit tangent vector to the track in
question, considered as a point on the unit circle. The degree of a
smooth map is equal modulo 2 to the number of inverse images of
a regular value [M]. For a regular value we choose $(-1,0)$, the horizontal
unit vector pointing left.
First, inspection of Fig. 10 shows that each
$B$ polygon contributes exactly one to the count of inverse images
of $(-1,0)$. With notation from the definition of polygonal impossible
configuration, the contribution of the $B$-polygons is $q$.
Next we will show that $(*)$ the $n_i$-gon $A_i$
contributes $n_i-2$ to this count. It will follow that the total
contribution of the $A$-polygons is $\sum_{i=1}^p (n_i - 2) = N-2p$.
Since $q=N-2p$, the grand total is the even number $2q$.
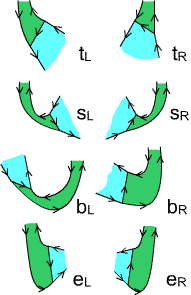
Fig. 11. The eight possible relative positions of an edge in an general-position oriented polygon: ${\bf t}_L, {\bf t}_R$ top left and right, ${\bf s}_L, {\bf s}_R$ side left and right, ${\bf b}_L, {\bf b}_R$ botton left and right and ${\bf e}_L, {\bf e}_R$ top-to-bottom left and right.
To prove $(*)$ note that an oriented $n$-gon in general position must fall in one of the three cases:2. The number of self-intersection points of an immersed oriented curve in the plane, counted mod 2, is one less than its rotation number. (Because the self-intersection number mod 2 is a regular homotopy invariant [W2], and because any curve with rotation number $n$ is regularly homotopic to $n$ turns of a spiral, with the endpoints joined [W1]: a curve with $|n|-1$ intersection points). So a curve with even rotation number must have an odd number of self-intersection points.
3. Let $\gamma_1, \dots, \gamma_k$ be the $k$ tracks of the path through our configuration. We know that the sum of their winding numbers is even, so an even number $\ell$ of them have odd winding number; these $\ell$ tracks each have even self-intersection number. The other $k-\ell$ tracks have even winding number and therefore odd self-intersection number. The sum of their self-intersection numbers is therefore congruent to $k-\ell$ and therefore to $k$, since $\ell$ is even; it follows that the sum of all the self-intersection numbers of the $\gamma_i$ is congruent mod 2 to $k$.
4. Finally, the self-intersection points of the path through the configuration, drawn as in Fig. 10, are of three types: those coming from the self-intersection numbers of $\gamma_i$ for $i=1,\dots,k$, those coming from intersections between $\gamma_i$ and $\gamma_j$ for $i\neq j$, and those coming from the intersections of the descending arms of the $B$-polygons. The second and third types come in pairs. So the total number of self-intersections is congruent mod 2 to $k$; and this must also hold for the number of those of the first two types, which is the number of vertices of the configuration.
Proof of Theorem 2.
Suppose the configuration, displayed as in Fig. 10, is not unicursal. Then by Theorem 1 it has at least three distinct paths; label them $I, J, K, \dots$ etc. Let us call the parts of the $B$-polygons that stretch down to the $A$ connectors; an $IJ$-connector will be one with path $I$ on the left, so leading away from the $B$-polygon in question, and $J$ on the right. We will see that two of the connectors can be switched (each attaching to the $A$-polygon edge formerly attached to the other) in such a way that the number of paths is reduced by 2. Iterating this process if necessary proves the proposition.
Assertion: There exist three paths $I, J, K$ such that
$P(IJK)$: the configuration has an $IJ$-connector and a $KI$-connector.
Proof of Assertion: Start
with $B_1$. We can suppose without loss of generality that $B_1$
is incident to at least two paths, so $B_1$ has an $IJ$-connector
with $I\neq J$. Now
End of proof:
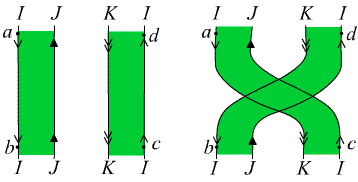
Fig. 12. The relevant part of the configuration, before and after the connectors have been switched.
After the connectors have been switched, $I, J$ and $K$ have been welded into a single path. Initially $I$ goes from $b$ to $c$ (out of the picture) and then from $d$ to $a$. Now between $c$ and $d$ the path also traverses the whole of $J$, and between $a$ and $b$ it traverses the whole of $K$.
Remark. The $(IJK)$ adjustment may change the genus of the resulting surface, because it also reconnects tracks of $\partial\mathcal{P}$. For example, when it is made on the 3-component configuration of Fig. 2c (genus 1) it yields the uncursal configuration of Fig. 2b (genus 0).