Неможливі конфігурації для геодезичних поверхонь із негативним викривленням (this page in Ukrainian).

Hass and Scott's example of a 4-valent graph on the 3-punctured sphere that cannot be realized by geodesics in any metric of negative curvature is generalized to impossible configurations filling surfaces of genus n with k punctures for any n and k.

Israel Journal of Mathematics volume 245, pages 165–172 (2021) Slightly longer arXiv version.

Here are some examples:

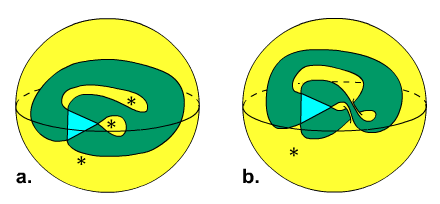
1. (a.) On the 3-punctured sphere. Vertices=3, Tracks=1. This is the Hass-Scott example.
(b.) On the punctured torus. Vertices=3, Tracks=3.

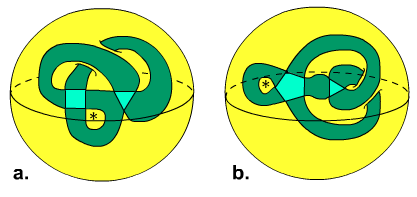
2. On the punctured torus. (a.) Vertices=7, Tracks=1. (b.) Vertices=8, Tracks=2.

3. On the 2-holed torus. Vertices=9, Tracks=1.