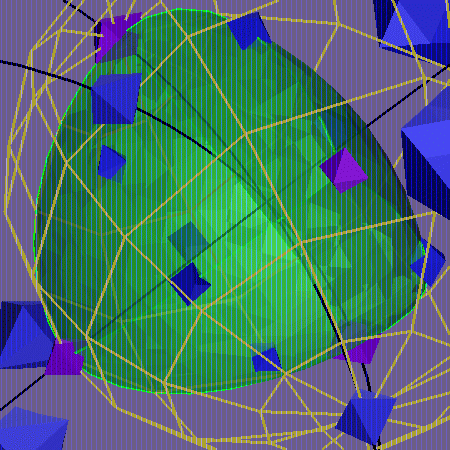
 In this conformal image
the yellow sphere is the equator between 1 and -1. We
are looking at it from the 1 side, so -1 is at the
center.
The tetrahedron is positioned with vertices i,j,k,a^2.
The four vertices are colored violet; the other group points
are colored blue. Here i is at the top of the picture,
j is on the left, k on the right and a^2 in the
foreground. The group elements -b,-c,-d are the midpoints
of the edges ia^2, ka^2 and ja^2 respectively, while
the elements b^2, c^2 and d^2 appear on the faces
jka^2, kia^2 and ija^2 respectively. The group element
-1 is in the interior of this tetrahedron.
In this conformal image
the yellow sphere is the equator between 1 and -1. We
are looking at it from the 1 side, so -1 is at the
center.
The tetrahedron is positioned with vertices i,j,k,a^2.
The four vertices are colored violet; the other group points
are colored blue. Here i is at the top of the picture,
j is on the left, k on the right and a^2 in the
foreground. The group elements -b,-c,-d are the midpoints
of the edges ia^2, ka^2 and ja^2 respectively, while
the elements b^2, c^2 and d^2 appear on the faces
jka^2, kia^2 and ija^2 respectively. The group element
-1 is in the interior of this tetrahedron.This is the largest of all the 12 possible spherical tetrahedra with vertices in the binary tetrahedral group. Its volume, 15/64, is almost 1/2 the volume of a hemisphere.