Notes on Second Order Differential Equations
Anthony Phillips -- Fall 1998
1. The general second order homogeneous linear differential
equation with constant coefficients looks like
2. The method of solution that we will work on involves
looking for an exponential-type solution
3. The solution of
![]() is
(``quadratic formula'')
is
(``quadratic formula'')
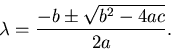
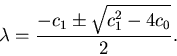
Example 1. If the differential equation is y''-y=0 (so c1=0 and c0=-1) the roots of the characteristic
equation
![]() are
are
![]() .
Both y=ex and y=e-x are solutions. (Check this!)
.
Both y=ex and y=e-x are solutions. (Check this!)
Example 2. If the differential equation is
y''+y'-2y=0 the roots of the characteristic
equation
![]() are
are
![]() ,
so
,
so
![]() and
and
![]() .
Both y=ex and y=e-2x are solutions. (Check this!)
.
Both y=ex and y=e-2x are solutions. (Check this!)
4. If the discriminant
c12-4c0 is negative, then the equation
![]() has no solutions, unless we enlarge the number field to include
has no solutions, unless we enlarge the number field to include
![]() ,
i.e. unless we work with complex numbers. If
c12-4c0=-k2 (we can write
any positive number as k2!) then ik is a square root of
c12-4c0since
(ik)2 = i2k2 = (-1)k2 = -k2. The solutions of the associated
algebraic equation are then
,
i.e. unless we work with complex numbers. If
c12-4c0=-k2 (we can write
any positive number as k2!) then ik is a square root of
c12-4c0since
(ik)2 = i2k2 = (-1)k2 = -k2. The solutions of the associated
algebraic equation are then
Example 3. If we start with the differential equation
y''+y=0 (so c1=0 and c0=1) the discriminant is
c12-4c0=-4,
so 2i is a square root of the discriminant and the solutions of the
characteristic equation are
![]() and
and
![]() .
.
Example 4. If the differential equation is
y''+2y'+2y=0 (so c1=2 and c0=2 and
c12-4c0=4-8 =-4). In this
case the solutions of the
characteristic equation are
![]() ,
i.e.
,
i.e.
![]() and
and
![]() .
.
5. Going from the solutions of the characteristic equation
to the solutions of the differential equation involves interpreting
![]() as a function of x when
as a function of x when ![]() is a complex number.
Suppose
is a complex number.
Suppose ![]() has real part a and imaginary part ib, so that
has real part a and imaginary part ib, so that
![]() with a and b real numbers. Then
with a and b real numbers. Then
6. Let us try this formula with our examples.
Example 3. For y''+y=0 we found
![]() and
and
![]() ,
so the solutions are
y1=eix and
y2=e-ix.
The formula gives us
,
so the solutions are
y1=eix and
y2=e-ix.
The formula gives us
![]() and
and
![]() .
.
Now here is a useful fact about linear differential equations: if y1and y2 are solutions of the homogeneous differential equation
y''+c1y'+c2y=0, then so is the linear combination
p y1 + q y2 for any numbers p and q. This fact is easy to check (just plug
p y1 + q y2 into the equation and regroup terms; note that the
coefficients a1 and a0 do not need to be constant for this to
work, that p and q can be complex as well as real constants, and
that this works for equations af any order).
Using this fact with the solutions from our example, we notice that
![]() and
and
![]() are both solutions. When we are given a problem with real
coefficients it is customary, and always possible, to exhibit real
solutions. Using the fact about linear combinations again, we can say
that
are both solutions. When we are given a problem with real
coefficients it is customary, and always possible, to exhibit real
solutions. Using the fact about linear combinations again, we can say
that
![]() is a solution for any p and q. This
is the general solution. (It is also correct to call
y=p eix +
q e-ix the general solution; which one you use depends on the context.)
is a solution for any p and q. This
is the general solution. (It is also correct to call
y=p eix +
q e-ix the general solution; which one you use depends on the context.)
Example 4.
y''+2y'+2y=0. We found
![]() and
and
![]() .
Using the formula we have
.
Using the formula we have
7. Repeated roots. Suppose the discriminant is zero:
c12-4c0 =0. Then the characteristic equation
![]() has one root. In this case both
has one root. In this case both
![]() and
and
![]() are solutions of the differential equation.
are solutions of the differential equation.
Example 5. Consider the equation
y''+4y'+4y=0. Here
c1 = c0 = 4. The discriminant is
![]() .
The only root is
.
The only root is
![]() .
Check that both e-2x and
x e-2x are solutions. The general solution is then
y = p e-2x + q x e-2x.
.
Check that both e-2x and
x e-2x are solutions. The general solution is then
y = p e-2x + q x e-2x.
8. Initial Conditions. For a first-order
differential equation the undetermined constant can be adjusted to
make the solution satisfy the initial condition y(0)=y0; in the
same way the p and the q in the general solution of a second
order differential equation can be adjusted to satisfy initial
conditions. Now there are two: we can specify both the value and
the first derivative of the solution for some ``initial'' value
of x.
Example 5. Suppose that for the differential
equation of Example 2,
y''+y'-2y=0, we want a solution with
y(0)=1 and y'(0)=-1. The general solution is
y=p ex + q e-2x, since the two roots of the characteristic
equation are 1 and -2. The method is to write down what the
initial conditions mean in terms of the general solution, and then
to solve for p and q. In this case we have
Example 6. For the differential equation of
Example 4,
y''+2y'+2y=0, we found the general solution
![]() .
To find a solution
satisfying the initial conditions y(0)=-2 and y'(0)=1
we proceed as in the last example:
.
To find a solution
satisfying the initial conditions y(0)=-2 and y'(0)=1
we proceed as in the last example: