Homework Solutions March 30

Ruben Costa Santos

Section 10.1

3. Is the folowing integral improper?

$$\int_{1}^{4} \frac{dx}{x^{2}\ln x}$$

The integral is improper because the integrand function is unbound when $x\rightarrow1$,

$$\lim_{x\rightarrow1} \frac{1}{x^{2} \ln x} = + \infty$$

10. Evaluate the improper integral:

$$\int_{e}^{\infty} \frac{dx}{x(\ln x)^2}.$$

Let us start by finding the antiderivative. Using the substitution $u=\ln x$ and du=dx/x we get:

$$\int \frac{dx}{x(\ln x)^2}=\int \frac{du}{u^2}=-\frac{1}{u}+C=-\frac{1}{\ln x}+C$$

Then integrating between e and t and taking the limit $t\rightarrow+\infty$ we find

$$\lim_{t\rightarrow+\infty} \int_{e}^{t} \frac{dx}{x(\ln x)^2}... ...im_{t\rightarrow+\infty} \left(-\frac{1}{\ln t}+1\right)=0+1=1$$

the limit exists and is finite so the integral is convergent.

11. Evaluate the improper integral

$$\int_{1}^{t} \frac{dx}{x(1+x)}.$$

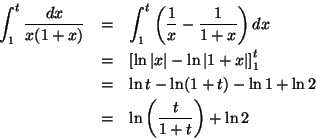
Let us consider the integral between 1 and a certain t>1 and then look at the limit $t\rightarrow+\infty$.

$$\begin{eqnarray*}\int_{1}^{t} \frac{dx}{x(1+x)} & = & \int_{1}^{t} \left(\frac{... ...) -\ln 1 +\ln 2 \\ & = & \ln \left(\frac{t}{1+t}\right) + \ln 2 \end{eqnarray*}$$

then:

$$\begin{eqnarray*}\lim_{t \rightarrow+ \infty} \int_{1}^{t} \frac{dx}{x(1+x)} & =... ...ty} \ln (\frac{t}{1+t}) + \ln 2 \\ & = & \ln 1 + \ln 2 = \ln 2 \end{eqnarray*}$$

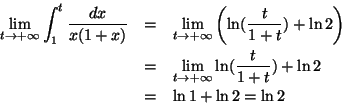
Notice that

$$\begin{eqnarray*}\lim_{t \rightarrow+ \infty} \ln (\frac{t}{1+t}) &=& \lim_{t ... ...1}{t}+1}\right) \\ &=& \ln \left(\frac{1}{0+1} \right)= \ln 1=0 \end{eqnarray*}$$

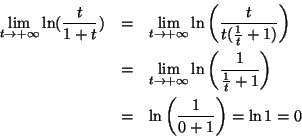
Since this limit exist the improper integral is convergente:

$$\int_{1}^{+ \infty} \frac{dx}{x(1+x)} = 1$$

14. Evaluate the improper integral

$$\int_{\pi}^{\infty} e^{-x} \sin x \,dx.$$

The antiderivative can be found be integration by parts in a similar way to example 8, page 497 of the book:

$$\begin{eqnarray*}\int e^{-x} sin x \,dx &=& -e^{-x} \sin x + \int e^{-x} \cos x ... ... \\ &=& -e^{-x} \sin x -e^{-x} \cos x -\int e^{-x} \sin x \,dx \end{eqnarray*}$$

in the first line we used:

$$\left\{ \begin{array}{l} u=\sin x \\ dv=e^{-x} dx \end{array}... ...egin{array}{l} du=\cos x \,dx \\ v=-e^{-x} \end{array} \right.$$

and from the fist to the second line:

$$\left\{ \begin{array}{l} u=\cos x \\ dv=e^{-x} dx \end{array}... ...gin{array}{l} du=-\sin x \,dx \\ v=-e^{-x} \end{array} \right.$$

then taking the last term in the right hand side to the left side we get:

$$\int e^{-x} sinx \,dx =\frac{-e^{-x}(\sin x +\cos x)}{2} + C$$

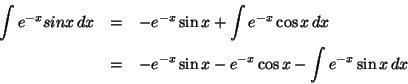
Now we integrate between $\pi$ and t:

$$\begin{eqnarray*}\int_{\pi}^{t} e^{-x} sinx \,dx &=&\left[\frac{-e^{-x}(\sin x +... ...& -e^{-t} \frac{(\sin t +\cos t)}{2} + e^{-\pi} \frac{(0-1)}{2} \end{eqnarray*}$$

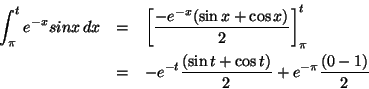
and take the limit $t\rightarrow\infty$

$$\lim_{t\rightarrow\infty} \int_{\pi}^{t} e^{-x} sinx \,dx = -\frac{e^{-\pi}}{2} = -0.0216\cdots$$

(remenber that $\lim_{t\rightarrow\infty} e^{-t} \cos t=\lim_{t\rightarrow\infty} e^{-t} \sin t=0$)

29. Evaluate the improper integral

$$\int_{0}^{8} \frac{dx}{x^{\frac{1}{3}}}.$$

The antiderivative is easy

$$\int \frac{dx}{x^{\frac{1}{3}}}=\int x^{-\frac{1}{3}}\,dx=\frac{3}{2}x^{\frac{2}{3}}+C$$

then integrate between a small $\varepsilon$ and 8 and take the limit

$$\lim_{\varepsilon\rightarrow\infty} \int_{\varepsilon}^{8} \f... ... \frac{3}{2}8^{\frac{2}{3}}=\frac{3}{2}(2^{3})^{\frac{2}{3}}=6$$

and we see that the integral converges to 6.

31.

Evalute the improper integral

$$\int_{2}^{3} \frac{x}{\sqrt{3-x}} dx.$$

Let us start by finding the antiderivative:

$$\begin{eqnarray*}\int \frac{x}{\sqrt{3-x}}dx &=& -\int \frac{3-x}{\sqrt{3-x}} dx... ... dx\\ &=& \frac{2}{3}(3-x)^{\frac{3}{2}}-6(3-x)^{\frac{1}{2}}+C \end{eqnarray*}$$

as you can check by differentiation.

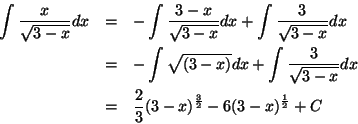
This time the integrand is unbound for $x\rightarrow3$ so we are interested in the limit

$$\begin{eqnarray*}\lim_{t\rightarrow3}\int_{2}^{t} \frac{x}{\sqrt{3-x}} dx &=& \l... ... &=& -\frac{2}{3} 1^{\frac{3}{2}}+6*1^{\frac{1}{2}}=\frac{16}{3} \end{eqnarray*}$$

The integral is convergent.

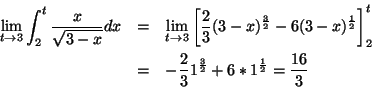
37. Evaluate the improper integral

$$\int_{-\infty}^{+\infty} \frac{dx}{e^{x}+e^{-x}}.$$

Let us start by fiding the antiderivative:

$$\begin{eqnarray*}\int \frac{dx}{e^{x}+e^{-x}}=\int \frac{dx}{e^{x}+\frac{1}{e^{x... ... \, dx \\ &=& \int \frac{du}{u^{2}+1} \\ &=& \arctan (e^{x})+C \end{eqnarray*}$$

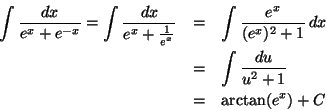
were we made the sustitution u=e^x and $du=e^{x}\,dx$.

The integral can be breaked into two parts and we look at them separately:

$$\int_{-\infty}^{+\infty} \frac{dx}{e^{x}+e^{-x}}= \int_{-\inf... ...{dx}{e^{x}+e^{-x}}+ \int_{0}^{+\infty} \frac{dx}{e^{x}+e^{-x}}$$

Let us look at the second part. We want to look at the limit

$$\begin{eqnarray*}\lim_{t\rightarrow\infty} \int_{0}^{t} \frac{dx}{e^{x}+e^{-x}}&... ...^{t}) -\arctan (0)\right)\\ &=& \frac{\pi}{2}-0= \frac{\pi}{2} \end{eqnarray*}$$

Remenber that $\tan (0)=0$ so $\arctan (0)=0$ and that $\lim_{x\rightarrow\pi/2} \tan (x)=+\infty$ so $\lim_{x\rightarrow+\infty}\arctan (x)=\pi/2$

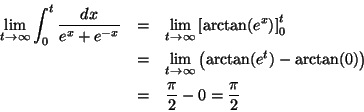
The limit for the other integral as exactly the same value, as you can see by doing it in the same way than above. This is not a surprise since the integrand is even in x (this means that f(x)=f(-x)) and we can relate the two integrals by a change of variavel u=-x and du=-dx :

$$\begin{eqnarray*}\int_{-t}^{0} \frac{dx}{e^{x}+e^{-x}}&=&-\int_{t}^{0} \frac{du}... ...ac{du}{e^{-u}+e^{u}}\\ &=& \int_{0}^{t} \frac{dx}{e^{-x}+e^{x}} \end{eqnarray*}$$

were from the second to the third line we just renamed u as x, or if you prefer did the trivial substitution x=u and dx=du.

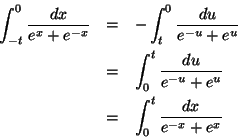
Then we conclude that the improper integral is convergent to the value

$$\lim_{t\rightarrow\infty} \int_{0}^{t} \frac{dx}{e^{x}+e^{-x}... ...^{0} \frac{dx}{e^{x}+e^{-x}}=\frac{\pi}{2} +\frac{\pi}{2}= \pi$$

41. a) Show that the improper integral $\int_{1}^{\infty} \frac{dx}{x}$ diverges. The antiderivative is just:

$$\int \frac{dx}{x}=\ln \vert x\vert +C$$

Then the limit

$$\lim_{t\rightarrow+\infty} \int_{1}^{t} \frac{dx}{x}= \lim_{t... ...y} \left[\ln \vert t\vert-\ln \vert 1\vert\right] = +\infty$$

is not finite and the integral is divergent.

b) Show that the $\int_{1}^{\infty} \frac{dx}{x^{p}}$ with p>1 converges.

Let us look, as usual, to the integral between 1 and a certain t:

$$\begin{eqnarray*}\int_{1}^{t} \frac{dx}{x^p}=\int_{1}^{t} x^{-p}\,dx&=& \left[ ... ...&=& \frac{1}{-p+1}\, \left(\frac{1}{t^{\vert-p+1\vert}}-1\right) \end{eqnarray*}$$

were you used the fact that -p+1<0 and then |-p+1|=-(-p+1), then taking the limit:

$$\lim_{t\rightarrow\infty} \int_{1}^{t} \frac{dx}{x^p}= \lim_{... ...1}\, \left(\frac{1}{t^{\vert-p+1\vert}}-1\right)=\frac{1}{1-p}$$

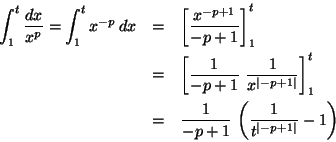
Since this the limit is finite the integral converges.

c) Show that the $\int_{1}^{\infty} \frac{dx}{x^{p}}$ with p<1 diverges.

The antiderivative is the same than above but now we have:

$$\int_{1}^{t} \frac{dx}{x^p}= \frac{1}{-p+1}\, \left(t^{\vert-p+1\vert}-1\right)$$

since -p+1>0 and then |-p+1|=-p+1. Then the limit

$$\lim_{t\rightarrow\infty} \int_{1}^{t} \frac{dx}{x^p}= \lim_{... ...ty} \frac{1}{-p+1}\, \left(t^{\vert-p+1\vert}-1\right)=+\infty$$

gives infinity and the integral is divergent.

44.a) Suppose that $f(x)\geq c\geq 0$ were c is a real number. Then the area from x=0 to x=t between the graph of f(x) and the x axis is larger then the area from 0 to t between the line y=c and the x axis. In terms of integrals:

$$\int_{1}^{t} f(x)\,dx \geq \int_{1}^{t}c\, dx =c\,(t-1)$$

then

$$\lim_{t\rightarrow+\infty} \int_{1}^{t} f(x)\,dx \geq \lim_{t\rightarrow+\infty} c\,(t-1) =+\infty$$

so the integral is divergent.

b) Now suppose that $0\leq g(x)\leq x^{-2}$. Then the area from x=1 to x=t between the graph of g(x) and the x axis is larger then the area from 1 to t between the graph of y=x^-2 and the x axis. In terms of integrals:

$$0\leq \int_{1}^{t} g(x)\,dx \leq \int_{1}^{t}x^{-2}\, dx =c\,(t-1)$$

We know from exercise 41.b) that the integral $\int_{1}^{+\infty}x^{-2}\, dx=1$ converges then the limit of the integral for $t\rightarrow+\infty$ must verify

$$0\leq \lim_{t\rightarrow+\infty} \int_{1}^{t} g(x)\,dx \leq 1$$

and exists because $\int_{1}^{t} g(x)\,dx$ is a increasing function of t. So the integral must be convergent.

c) Suppose that $h(x)\geq x^{-1}$ for $x\geq 1$. Then we must have, following the same reasoning on the areas, that

$$\int_{1}^{t} h(x)\,dx \geq \int_{1}^{t}x^{-1}\, dx$$

but we know from exercise 41.c) that the integral $\int_{1}^{\infty}x^{-1}\, dx$ is divergent then, in a similar way than above, we see that $\int_{1}^{\infty} h(x)\,dx$must also be divergent.