Section 7.4

4) The exact value of the integral is easy to obtain.

Let's compare this to the approximation obtained with Simpson's rule, . To subdivide the interval into 2 subintervals, we need 3 equally spaced points Define h=(b-a)/2.

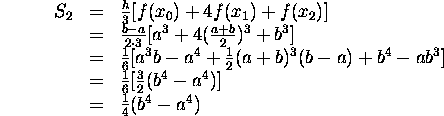
As we can see, the approximation given by Simpson's rule is in fact the exact value of the definite integral.

6)

a) To evaluate , we need 5 equally spaced points in the interval [a,b]=[0,2]. If then .

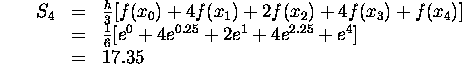
b) Theorem 4 in Section 7.4 provides an upper bound for the approximation error

n is 4 in our case and is an upper bound for , which we still need to determine.

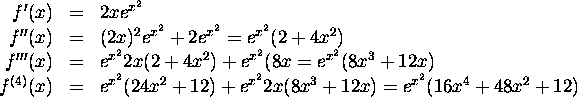
We need to find the largest value of for . A graph could be used to determine the smallest and largest values of . We will instead define and use the standard techniques of calculus to identify the maxima and minima of g.

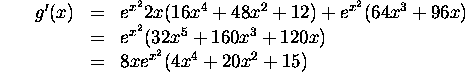
It is easy to see that because only even powers of x occur. g'(x) > 0 on the interval (0,2] and therefore g is increasing. Notice moreover that and g increases for the rest of the interval. The largest value of is therefore attained at x=2. If then will be an upper bound. Plugging everything back into our original inequality

.

e) We need to find a condition on n that will guarantee that . Consider that

Using algebra, we see that when the error is as desired.

9) We have the following inequalities

where I is the exact value of indefinite integral. These inequalities can be justified with a picture. For each one of the methods, draw the rectangle or trapezoid that is used to estimate the area above a single subinterval .

Unfortunately, it is impossible to determine where belongs in this sequence of inequalities. It is clear that because is a weighted average of and ,

that belongs in between and . Nothing about can stated with such certainty.

11) In this case h=(b-a)/n=3/4 and f is given at all the points .

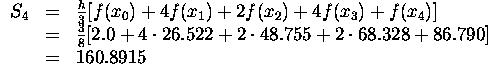
An upper bound for is obviously .

Section 8.1

4) a) I redrew the curve using an identical scale for the x and y axis. I then placed a shoelace on top of the curve and measured the length of the string with a ruler. I obtained 72 mm as an estimate for the length. My scale on the bottom of the graph was 1 unit = 50 mm. 72 mm was therefore equivalent to 1.44 units.

b) Using the trapezoid rule with 2 subdivisions, we can give the area under the curve an eyeball estimate of 1.47 units.

c) The only error bound available for the midpoint rule is given in Section 7.4, Theorem 3, as

where

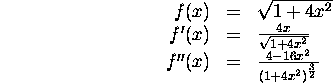
For ,

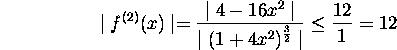
where we have made the numerator as large as possible (x=1) and the denominator as small as possible (x=0). Plugging this information into our inequality we obtain

d) Before we apply identity 35 in the book we will manipulate the integrand in order to put it into a convenient form.

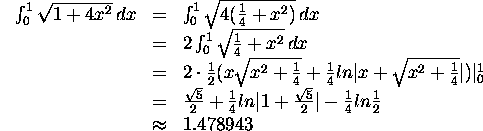
Section 8.2

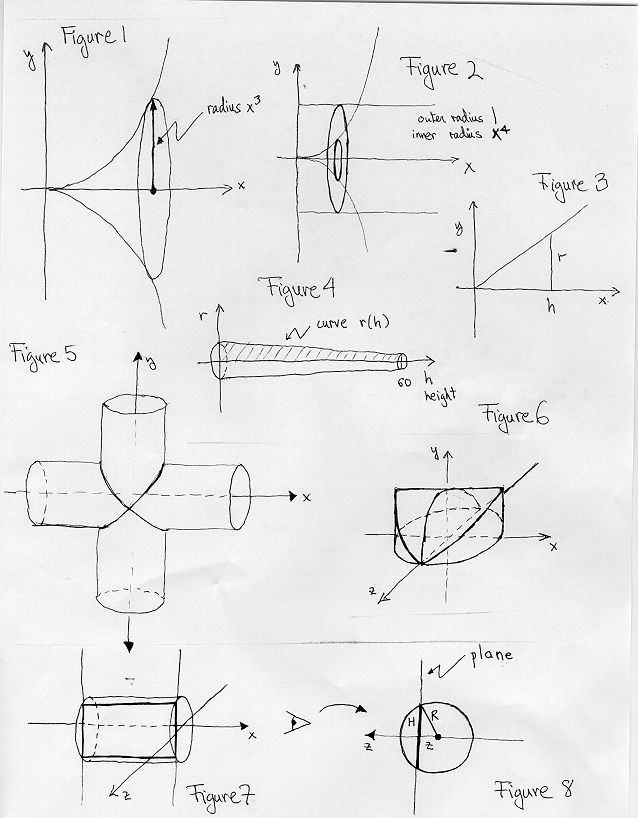
1) See Figure 1 (at bottom) for a picture of the solid of revolution. Each cross-section of the solid, at x, is a circle of radius . We therefore have . Cross-sections of the volume are taken at each .

2) See Figure 2 (at bottom) for a picture of the solid of revolution. Each cross-section of the solid, at x, is a ``washer''. The outer radius of the washer is 1 and the inner radius is . The area of the washer is therefore given by

The region bounded is bounded on the left and the right by respectively. The integration is therefore performed from 0 to 1.

9) Consider the line . The graph of this line is given in Figure 3 (at bottom). If the region below the curve and between x=0,x=h is rotated around the x-axis, we obtain the cone mentionned in the question. For , the cross-section is a circle of radius rx/h and its area is

17) If at each height, we knew the radius of the pole, r(h), then we could make a picture like Figure 4 (at bottom). This picture shows that we could obtain the volume of the pole as the volume of the solid of revolution about the h-axis for the curve r. Cross-sections at h would be be circles of radius r and their area would be

This last integral will be approximated with Simpson's rule but first we need to derive an expression for r(h). We only know the circumference, C, at a given height, . The relationship between radius and circumference of a circle is

Let's build a new table of values using the right-hand side identity.

The interval [0,60] is subdivided into 6 subintervals of length h=10.

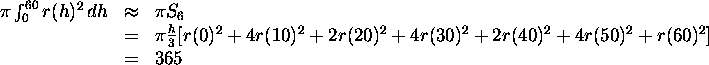
26) Figure 5 (at bottom) is useful to identify the axes. Figure 6 is a sketch of the top half of the intersection of the two full cylinders. A cross-section taken perpendicularly to the z-axis is clearly a square. The top and bottom edges of the square are the intersection of the plane (perpendicular to the z-axis) and the horizontal cylinder. In Figure 7, the dark outline of a rectangle indicates the position of the intersection of this plane with the full cylinder. To calculate the lenght of the vertical edges of the square we will try to obtain the distance between the two horizontal edges. These two horizontal edges are clearly identified in Figure 7 as the edges of the intersection of the plane and the surface of the cylinder. Figure 8 is a cross-section perpendicular to the x-axis of the horizontal cylinder intersecting our plane. The strip has width 2H where, according to Pythagoras's theorem,

for .

This shows that one of the sides of the original square cross-section is

The area of the cross-section is therefore . To every there corresponds a unique cross-section and so we must integrate from -R to R.

Tony Phillips
Fri Feb 20 12:40:37 EST 1998