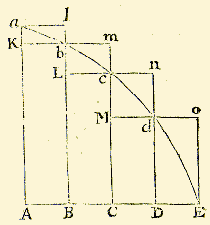
Illustration from Newton's Principia for his proof that for a monotonic
function f defined on an interval [A,E] the difference between the upper
and lower sums with n equal subdivisions is equal in absolute value to
(f(E)-f(A))(E-A)/n (and therefore goes to 0 as n goes to infinity). Here n=4.
SUNY at Stony Brook -- Calculus II -- Spring 1998
