The heat equation in a laterally insulated bar of length 2
with fixed
temperature at one end (![]() ) and insulated at the other (
) and insulated at the other (![]() ) leads to the eigenvalue problem
) leads to the eigenvalue problem
- (20 points)
Calculate the eigenvalues and eigenfunctions for this problem.
- (10 points)
Are these eigenfunctions orthogonal, i.e. does
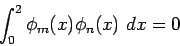
where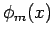 and
and 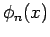 are eigenfunctions corresponding
to two eigenvalues
are eigenfunctions corresponding
to two eigenvalues
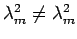 ? Explain your answer
carefully.
? Explain your answer
carefully.
- (15 points)
Are the eigenfunctions for this problem orthogonal, i.e. does
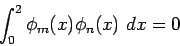
where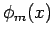 and
and 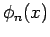 are eigenfunctions corresponding
to two eigenvalues
are eigenfunctions corresponding
to two eigenvalues
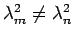 ? Explain your answer
carefully.
? Explain your answer
carefully.
- (20 points)
Calculate the first (the smallest positive) eigenvalue for this problem.
The vibrations of a cord of length 2 fixed at both ends are governed by the wave equation
Suppose that at ![]() the cord is not moving, i.e.
the cord is not moving, i.e.
![]() , and that the graph of the initial position
function
, and that the graph of the initial position
function ![]() shows two adjacent equilateral triangles of
base 1,
like
shows two adjacent equilateral triangles of
base 1,
like ![]() .
.
- (25 points)
Sketch the d'Alembert solution of this problem for
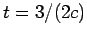 .
.
- (10 points)
The sound spectrum of the resulting vibration will have
a component at frequency
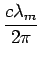 if the eigenfunction corresponding to
if the eigenfunction corresponding to 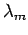 occurs with
non-zero coefficient in the eigenfunction expansion of
occurs with
non-zero coefficient in the eigenfunction expansion of 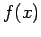 .
Which frequencies will be heard in the vibration of the cord with
this initial condition?
.
Which frequencies will be heard in the vibration of the cord with
this initial condition?