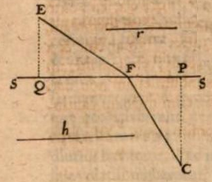
Given two points C and E and a line SS in the same plane as them, one seeks a point F on the line SS such that when CF and EF are drawn the sum of the rectangles, GF and a given line $h$ and FE and a given line $r$ are as small as possible. In other words, if SS is a line separating two media, and $h$ represents the density of the medium (like water) on the side of C, $r$ that of the medium (like air) on the side of E, then we ask for the point F such that the path from C to E via F is the easiest possible.
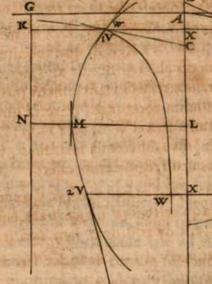
Let us suppose all such possible sums of rectangles, or all the difficulties of possible paths, to be represented by the ordinates KV (of a curve VV) perpendicular to the line GK. We shall call these ordinates $w$. Then it is required to find their minimum NM.
Since C and E are given, we also have: their perpendiculars to SS, namely CP (which we will call $c$) and EQ (which [we will call] $e$); along with PQ (which [we will call] $p$). We denote QF = GN (or AL [Leibniz has AX]) by $x$, CF by $f$ , and EF by $g$ . Then FP $= p - x$; and $ f = \sqrt{cc + pp - 2px + xx}$ or $\sqrt{l}$ for short; and $g = \sqrt{ee + xx}$ or $\sqrt{m}$ for short. We therefore will have $w=h\sqrt{l}+r\sqrt{m}$. The differential equation (since $dw = 0$ in the case of a minimum) is ${\displaystyle 0=-\frac{h dl}{2\sqrt{l}}-\frac{r dm}{2\sqrt{m}}}$, by the rules of our calculus; now $dl$ is $-2dx(-p+x)$, and $dm$ is $2x dx$, hence ${\displaystyle \frac{h(p-x)}{f}=\frac{rx}{m}}.$ When we now apply this to dioptrics, and take $f$ and $g$, that is, CF and EF, equal to each other (since the refraction at the point F is the same no matter how long we set the line GF to be), then $h(p - x) = rx$ or ${\displaystyle \frac{h}{r} = \frac{x}{p-x}}$ or $h$ is to $r$ as QF is to FP; this means that the sines of the angles of incidence and of refraction, FP and QF, are in inverse ratio to $r$ and $h$ , the densities of the media in which the incidence and the refraction take place. However, this density is not to be understood with respect to us, but as the resistance which the light rays meet. Thus we have a demonstration of the computation exhibited elsewhere in these Acta [1682], when we presented a general foundation of optics, catoptrics, and dioptrics. Other very learned men have sought in many devious ways what someone versed in this calculus can accomplish in three lines.
This translation is adapted from the one in D. J. Struik, A Source Book in Mathematics, 1200-1800.Re the last sentence of the argument: the angles of incidence and refraction are measured from the perpendicular to SS at F, and remember that the ray is incident from below. So sin(ang. inc.) = cos($<$PFC) = FP/$g$, and sin(ang. ref.) = cos($<$QFE) = QF/$f$ = QF/$g$ by our assumption. Hence sin(ang. inc.)/sin(ang. ref.) = FP/QF = $r/h$.