The True History of the Law of Cosines.
In a nutshell, Al-Battani had the equipment, but did not formulate the law.
He works in astronomical, not geometric terms. It is true
that to go from one of his formulas to the law of cosines you only have to
write the length of the day in terms of the latitude and the
height of the Ecliptic; this he certainly could have done, but he did not.
Here are the details, as explained by Anton von Braunmühl in his
Vorlesungen über Geschichte der Trigonometrie.

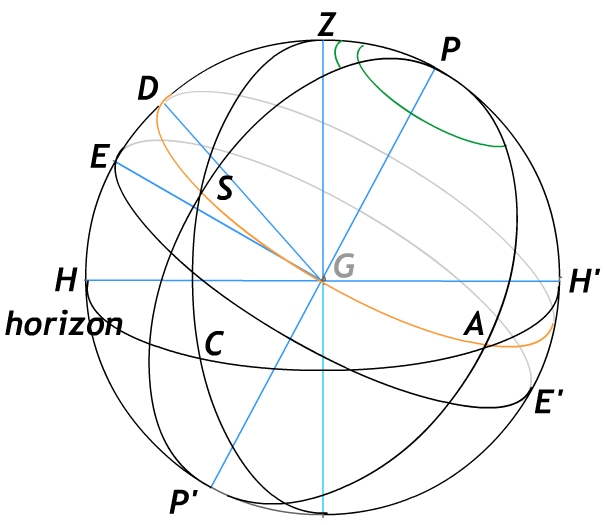
This image is adapted from Braunmühl's Fig. 15. It is
based on Al-Battani and presumably shows
the calculation of the height
![]() of the sun at a given time
of the sun at a given time
![]() .
.
As represented, the celestial sphere intersects the plane of
the figure in the great circle containing the poles ![]() and the mid-day position
and the mid-day position ![]() of the Sun. The Sun rises
at
of the Sun. The Sun rises
at ![]() . The surface angle
. The surface angle ![]() =
= ![]() is
is ![]() the length of the day. The surface angle
the length of the day. The surface angle ![]() gives
the time
gives
the time ![]() of the observation, measured from noon. The
other quantities entering into the calculation are
the colatitude
of the observation, measured from noon. The
other quantities entering into the calculation are
the colatitude
![]() and the (complement of the)
angle of the Earth's axis with the Ecliptic, measured by
and the (complement of the)
angle of the Earth's axis with the Ecliptic, measured by
![]() . Al-Battani's formula is given in terms of the sinvers function,
equivalent to our cosine:
. Al-Battani's formula is given in terms of the sinvers function,
equivalent to our cosine:
![]() , and
reads as follows:
, and
reads as follows:
This is described by Braunmühl, footnote 1 on page 53. He goes on to
say that this is not quite the spherical law of cosines.
The statement that Al-Battani ``knew'' the law of cosines he quotes from
H. Hankel: ``Vor den trigonometrischen Fundamentalsätzen kennt
Al-Battáni außer denen des Almagest bereits die Formel
Braunmühl continues: Aber weder die erste, noch die zweite dieser Formel kommt bei ihm irgendwo vor. Hankel's Irrtum scheint mir aus Delambre's Hist. de l'Astr. du moyen age p. 20 zu stammen, denn dieser führt dort in die bei Al-Battáni vorkommende Gleichung
statt
![]() den Wert
den Wert
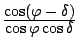 ein, wodurch sie dann allerdings in
ein, wodurch sie dann allerdings in
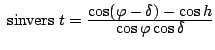 übergeht. Aber diese Substitution hat Delambre,
nicht Al-Battáni ausgeführt, der überhaupt nirgends mit
Gleichungen rechnet, sodaß bei ihm von einem Zusammenhang dieser
Formeln, oder besser Regeln, untereinander nirgends eine Spur vorhanden
ist.
übergeht. Aber diese Substitution hat Delambre,
nicht Al-Battáni ausgeführt, der überhaupt nirgends mit
Gleichungen rechnet, sodaß bei ihm von einem Zusammenhang dieser
Formeln, oder besser Regeln, untereinander nirgends eine Spur vorhanden
ist.
Braunmühl also makes the important remark (page 54) that there is
no mention of the spherical triangle ![]() in Al-Battáni. (... ohne
irgendwelche Beziehung auf das sphärische Dreieck
in Al-Battáni. (... ohne
irgendwelche Beziehung auf das sphärische Dreieck ![]() .)
.)
In his section on Regiomontanus (pp 130-133) Braunmühl gives evidence that R. was well acquainted with Al-Battáni's work, and states ``kein Zweifel mehr bestehen kann, daß er beim Studium des Albategnius zu diesem Lehrsatze geführt wurde.'' But he also says (still about the law of cosines) ``Dieses Verdienst muß nach unserer Ansicht Regiomontan ganz allein zugesprochen werden.''