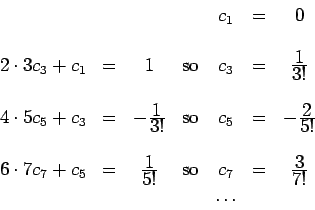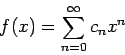Next: About this document ...
Stony Brook University MAT 127 Calculus C
Power series solutions for initial-value problems.
The Method. Power series give a very general method for
solving initial-value problems. For convenience in notation, we will take the
initial value or values to be given at 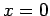 .
.
An initial-value problem that we cannot solve with this term's methods
is
(This problem models a harmonic oscillator with period 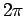 starting from rest and being driven at its natural
frequency).
starting from rest and being driven at its natural
frequency).
The power series method consists in taking 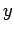 to be given by an unknown
power series in
to be given by an unknown
power series in 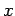 :
:
and then using the equation and the initial conditions to solve for
the coefficients
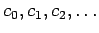 . Here it is immediate that
. Here it is immediate that
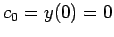 , and that
, and that
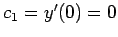 , but the equation
will force relations between the
, but the equation
will force relations between the 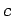 s which allow them all to
be calculated.
s which allow them all to
be calculated.
Differentiating the power series twice, term by term, we get:
Now we can write 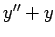 as a single power
series by adding the coefficients of like powers as usual:
as a single power
series by adding the coefficients of like powers as usual:
We know 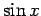 has the Maclaurin series
has the Maclaurin series
so our differential equation becomes an equation between two
power series. The two sides of the equation
can be equal
for all values of 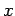 only if all
like coefficients on left and right are equal.
This gives a system of equations:
only if all
like coefficients on left and right are equal.
This gives a system of equations:
We already know 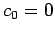 and
and 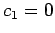 from our initial conditions.
Furthermore the equations for even indices all have right-hand side 0;
and since
from our initial conditions.
Furthermore the equations for even indices all have right-hand side 0;
and since 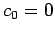 , it follows that
, it follows that 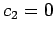 , so
, so 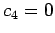 , ... . All the
even-indexed coefficients are 0.
For the odd coefficients we may solve the system recursively:
, ... . All the
even-indexed coefficients are 0.
For the odd coefficients we may solve the system recursively:
This pattern will continue, as can easily be checked, giving
It follows from the ratio test that the function given by
with these coefficients is defined for all values of 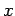 . It is the
solution to our initial value problem.
. It is the
solution to our initial value problem.
In certain cases it is possible to identify the solution in terms
of known functions. This particular initial value problem
can also be solved by the method
of variation of parameters, yielding the solution:
The Maclaurin series for this 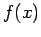 is exactly the series
we calculated.
is exactly the series
we calculated.
Exercises:
- Verify that the Maclaurin series for
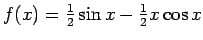 is exactly the power series we calculated
as solution to
is exactly the power series we calculated
as solution to
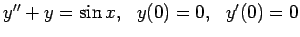 .
.
- Use the power series method to solve the initial value
problem
and identify the solution as an elementary function.
- Use the power series method to solve the initial value
problem
and identify the solution as before.
- Use the power series method to solve the initial value
problem
and identify the solution as an elementary function.
- Use the power series method to solve the initial value
problem
and identify the solution as an elementary function.
- Use the power series method to solve the initial value
problem
and identify the solution in terms of elementary functions.
- Use the power series method to solve the initial value
problem
(consider 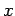 as a power series with
as a power series with 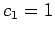 and all other
coefficients zero)
and identify the solution as the power series of
and all other
coefficients zero)
and identify the solution as the power series of
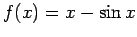 .
.



Next: About this document ...
Tony Phillips
2007-01-08
![]() .
.
![]() starting from rest and being driven at its natural
frequency).
starting from rest and being driven at its natural
frequency).
![]() to be given by an unknown
power series in
to be given by an unknown
power series in ![]() :
:
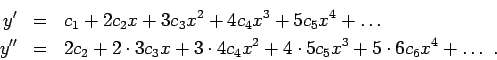
![]() as a single power
series by adding the coefficients of like powers as usual:
as a single power
series by adding the coefficients of like powers as usual:
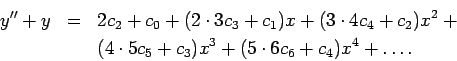
![]() has the Maclaurin series
has the Maclaurin series
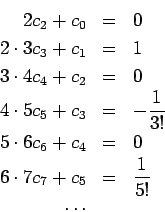
![]() and
and ![]() from our initial conditions.
Furthermore the equations for even indices all have right-hand side 0;
and since
from our initial conditions.
Furthermore the equations for even indices all have right-hand side 0;
and since ![]() , it follows that
, it follows that ![]() , so
, so ![]() , ... . All the
even-indexed coefficients are 0.
For the odd coefficients we may solve the system recursively:
, ... . All the
even-indexed coefficients are 0.
For the odd coefficients we may solve the system recursively: