MAT511 homework, due Oct 22, 2003
- Let
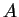 and
and 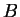 be nonempty sets. Prove that
be nonempty sets. Prove that
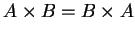 if and only if
if and only if 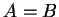 . What if one of
. What if one of 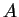 or
or 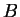 is empty?
is empty?
- For each of the relations below, indicate whether it is reflexive,
symmetric, or transitive. Justify your answer.
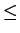 on the set
on the set
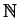 .
.
-
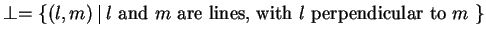 .
.
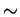 on
on
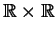 , where
, where
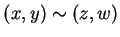 if
if
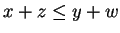 .
.
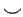 on
on
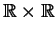 , where
, where
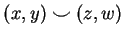 if
if
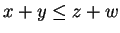 .
.
 on
on
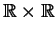 , where
, where
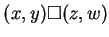 if
if 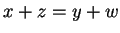 .
.
- Prove that if
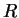 is a symmetric, transitive relation on a set
is a symmetric, transitive relation on a set 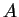 ,
and the domain of
,
and the domain of 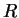 is
is 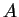 , then
, then 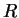 is reflexive on
is reflexive on 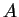 .
.
- Consider the relations
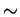 and
and  on
on
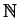 defined by
defined by 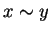 iff
iff 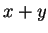 is even, and
is even, and
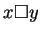 iff
iff 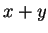 is a multiple of 3.
Prove that
is a multiple of 3.
Prove that 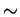 is an equivalence relation, and that
is an equivalence relation, and that  is not.
is not.
- For each
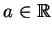 , let
, let
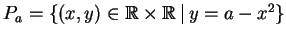 .
.
- Sketch the graph of
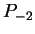 ,
, 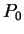 , and
, and 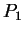 .
.
- Prove that
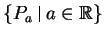 forms a partition of
forms a partition of
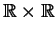 .
.
- Describe the equivalence relation associated with this
partition.
Scott Sutherland
2003-10-17
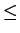 on the set
on the set
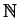 .
.
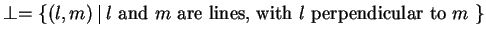 .
.
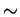 on
on
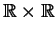 , where
, where
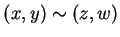 if
if
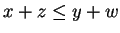 .
.
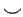 on
on
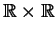 , where
, where
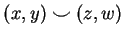 if
if
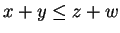 .
.
 on
on
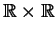 , where
, where
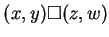 if
if 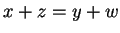 .
.
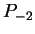 ,
, 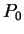 , and
, and 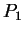 .
.
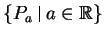 forms a partition of
forms a partition of
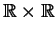 .
.