MAT511 homework, due Dec. 3, 2003
- Recall that in class (and in the handout copied from Eves;
alternatively, a similar discussion can be found at
http://www.shu.edu/projects/reals/logic/numbers.html
),
we considered the equivalence relation on
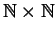 given by
given by
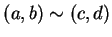 whenever
whenever
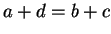 . We said that the set of
equivalence classes corresponded to the integers
. We said that the set of
equivalence classes corresponded to the integers
 , where the
each natural number
, where the
each natural number 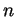 corresponds to equivalence class with
elements of the form
corresponds to equivalence class with
elements of the form 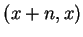 while negative integers correspond to
classes of the form
while negative integers correspond to
classes of the form 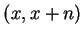 .
.
Show that the relation 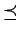 given by
given by
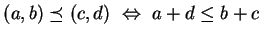 defines a total order on the equivalence classes, which
corresponds to the usual notion of order on
defines a total order on the equivalence classes, which
corresponds to the usual notion of order on
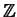 . (Recall that a
total order is a partial order in which all elements are comparable.)
. (Recall that a
total order is a partial order in which all elements are comparable.)
- If
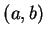 and
and 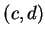 are representatives of two equivalence
classes as above, we can define multiplication as
are representatives of two equivalence
classes as above, we can define multiplication as
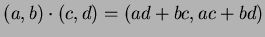 . Remember that these are
equivalence classes, so the statement
. Remember that these are
equivalence classes, so the statement
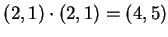 means
means
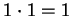 .
.
Using this definition, show that if 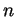 and
and 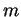 are negative
integers,
are negative
integers, 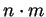 is a positive integer.
is a positive integer.
- We discussed how each real numbers corresponds to a Dedekind cut,
or an infinite decimal that doesn't end in all 9s. Let
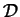 be the set of all real numbers greater than 0 and less than 1 which
don't use the digits 1, 3, 5, 7, or 9 in their decimal expansion.
Show that
be the set of all real numbers greater than 0 and less than 1 which
don't use the digits 1, 3, 5, 7, or 9 in their decimal expansion.
Show that
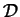 is an uncountable set.
is an uncountable set.
- Let
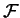 be the set of all functions from
be the set of all functions from
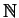 to
to
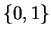 .
What is the cardinality of
.
What is the cardinality of
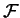 ? Hint: You might find it
conceptually easier to first think about the set
? Hint: You might find it
conceptually easier to first think about the set
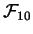 of all
functions from
of all
functions from
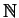 to
to
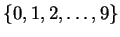 ;
;
 and
and
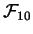 have the same cardinality.
have the same cardinality.
Scott Sutherland
2003-11-23
![]() given by
given by
![]() defines a total order on the equivalence classes, which
corresponds to the usual notion of order on
defines a total order on the equivalence classes, which
corresponds to the usual notion of order on
![]() . (Recall that a
total order is a partial order in which all elements are comparable.)
. (Recall that a
total order is a partial order in which all elements are comparable.)
![]() and
and ![]() are negative
integers,
are negative
integers, ![]() is a positive integer.
is a positive integer.