The Logistic Map for a>4
adapted from section 1.6 of
An Introduction to Chaotic Dynamical Systems, by Robert Devaney

We now consider the behavior of

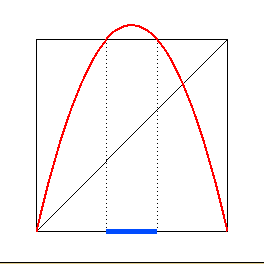For the remainder of this section, we will usually drop the subscript a and write F instead of . As before, all of the interesting dynamics of F occur in the unit interval I = [0,1]. Note that, since a > 4, the maximum value of F is larger than one. Hence certain points leave I after one iteration of F. Denote the set of such points by . Clearly, is an open interval centered at 1/2 and has the property that, if then F(x) > 1, so and . is the set of points which immediately escape from I. All other points in I remain in I after one iteration of F.

Let If , then , , and so, as before, . Inductively, let . That is,

so that consists of all points which escape from I at the iteration. As above, if x lies in , it follows that the orbit of x tends eventually to . Since we know the ultimate fate of any point which lies in the , it remains only to analyze the behavior of those points which never escape from I, i.e., the set of points which lie in

Let us denote this set by A. Our first question is: what precisely is this set of points? To understand A, we describe more carefully its recursive construction.

Since is an open interval centered at 1/2, consists of two closed intervals, on the left and on the right.

Note that F maps both and , monotonically onto I; F is increasing on and decreasing on . Since , there are a pair of open intervals, one in and one in , which are mapped into by F. Therefore this pair of intervals is precisely the set .

Now consider . This set consists of 4 closed intervals and F maps each of them monotonically onto either or . Consequently maps each of them onto 1. Thus, each of the four intervals in contains an open subinterval which is mapped by onto . Therefore, points in these intervals escape from I upon the third iteration of F. This is the set we called . For later use, we observe that is alternately increasing and decreasing on these four intervals. It follows that the graph of must therefore have two ``humps''.

Continuing in this manner we note two facts. First, consists of disjoint open intervals. Hence consists of closed intervals since

Secondly, maps each of these closed intervals monotonically onto I. In fact, the graph of is alternately increasing and decreasing on these intervals. Thus the graph of has exactly humps on I, and it follows that the graph of crosses the line y = x at least times. This implies that has at least fixed points or, equivalently, Per(F) consists of points in I. Clearly, the structure of A is much more complicated when a > 4 than when a < 3.

The construction of A is reminiscent of the construction of the Middle Thirds Cantor set: A is obtained by successively removing open intervals from the "middles" of a set of closed intervals. See section 4.1 of Alligood, Sauer, & Yorke and/or Neal Carothers' Cantor Set web pages for more details.

Definition: A set is a Cantor set if it is a closed, totally disconnected, and perfect subset of an interval. A set is totally disconnected if it contains no intervals; a set is perfect if every point in it is an accumulation point or limit point of other points in the set.

Example: The Middle-Thirds Cantor Set. This is the classical example of a Cantor set. Start with [0,1] but remove the open "middle third," i.e. the interval . Next, remove the middle thirds of the resulting intervals, that is, the pair of intervals and . Continue removing middle thirds in this fashion; note that open intervals are removed at the stage of this process. Thus, this procedure is entirely analogous to our construction above.

Remark. The Middle-Thirds Cantor Set is an example of a fractal. Intuitively, a fractal is a set which is self-similar under magnification. In the Middle-Thirds Cantor Set, suppose we look only at those points which lie in the left-hand interval . Under a microscope which magnifies this interval by a factor of three, the "piece" of the Cantor set in looks exactly like the original set. More precisely, the linear map L(x) = 3x maps the portion of the Cantor set in homeomorphically onto the entire set.

This process does not stop at the first level: one may magnify any piece of the Cantor set contained in an interval by a factor of to obtain the original set.

To guarantee that our set A is a Cantor set, we need an additional hypothesis on a. Suppose a is large enough so that | F'(x)| > 1 for all . The reader may check that suffices. Hence, for these values of a, there exists such that for all . By the chain rule, it follows that as well. We claim that A contains no intervals. Indeed, if this were so, we could choose two distinct point x and y in A with the closed interval . Notice that for all . Choose n so that . By the Mean Value Theorem, it then follows that , which implies that at least one of or lies outside of I. This is a contradiction, and so A is totally disconnected.

Since A is a nested intersection of closed intervals, it is closed. We now prove that A is perfect. First note that any endpoint of an is in A: indeed, such points are eventually mapped to the fixed point at 0, and so they stay in I under iteration. Now if a point were isolated, every near point near p must leave I under iteration of F. Such points must belong to some . Either there is a sequence of endpoints of the converging to p, or else all points in a deleted neighborhood of p are mapped out of I by some power of F. In the former case, we are done as the endpoints of the map to 0 and hence are in A. In the latter, we may assume that maps p to 0 and all other points in a neighborhood of p into the negative real axis. But then has a maximum at p so that . By the chain rule, we must have for some i < n. Hence , and so is not in I, contradicting the fact that .

Hence we have proved

Theorem. If , then A is a Cantor set.

Remark. The theorem is true for a > 4, but the proof is more delicate. Essentially, all we need is that for each , there is an N such that for all , we have . Then almost exactly the same proof applies.

We have now succeeded in understanding the gross behavior of orbits of when a > 4. Either a point tends to under iteration of ,or else its entire orbit lies in a Cantor set A. For points , we see the same complicated type of behavior that we have seen for a=4: there are periodic points of all periods, but even more: we can symbolically specify a behavior by a string of Rs and Ls, and such an orbit necessarily exists. We will return to this issue later.

• About this document ...