Putting together geometric shapes (as in the Sierpinski gasket and
vonKoch snowflake) is not the only way to construct self-similar
fractals. We can apply the same idea to familiar analytic functions.
Consider the function f(x) defined as follows:
f:=x->sum(cos(2^k*x)/(1.5)^k,k=0..NumTerms);
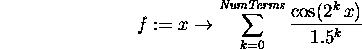
Certainly the sum converges for all x (because we are adding terms
whose absolute value is smaller than a geometric series of ratio 1.5),
so f(x) is well defined, even if we take NumTerms to be infinity.
Unfortunately, for arbitrary values of x, the infinite sum is
difficult to evaluate. We'll truncate the sum after, say, 50 terms.
NumTerms:=50:
This isn't a problem, since the resulting function is off from the
"real one" by at most
sum(1/(1.5)^k,k=(NumTerms+1)..infinity);
.000000003136657091
which is certainly small enough for us to neglect here.
Why should we expect the graph of the function to be self-similar? We can think of the sum as telling us how to build the function iteratively, with each additional term giving us the next "level", just as we did for the previous fractals. At each stage, we take the graph we had before, and push it around by a small copy of the cosine graph. (Notice that the period of cos(2^k*x) is half that of cos(2^(k-1)*x), so we're doubling the number of "wiggles". Also, we decrease the height of the added wiggles by 2/3 each time. This is almost the same idea as what we did with the geometric objects.
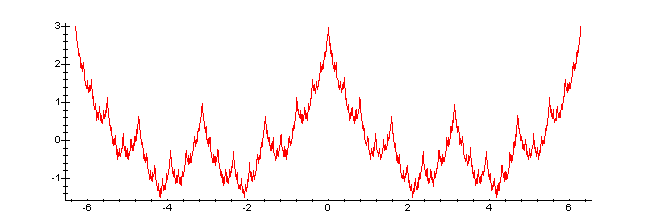
Enough chatting. Let's see what the function looks like.
plot(f(x),x=-2*Pi..2*Pi,numpoints=1001,axes=framed);

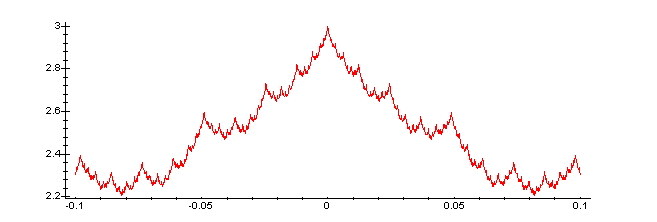
Just to emphasise the self-similarity, lets compare two small pieces
of the graph.
plot(f(x),x=-0.1..0.1,numpoints=1001,axes=framed);
plot(f(x),x=-.00078..0.00078,numpoints=1001,axes=framed);
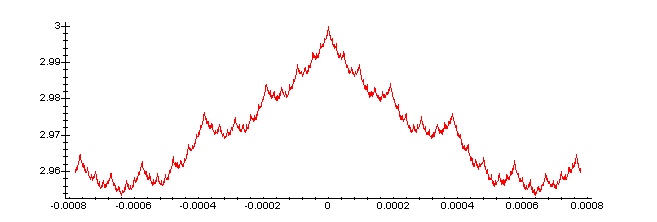
Despite the fact that the second graph is over a domain about 125 times smaller than the upper, the two graphs (after rescaling) are nearly identical. Also notice that the choice of the rescaling factors were somewhat arbitrary (as was the use of cosine... just about any bounded function should work, although being periodic makes things easier). What do you think would happen to the dimension of the graph if we change the 1.5^k to 2^k?