MAT331
Exercise 3: Simple Cryptography
- 1.
- Decode the following phrase, which was encoded using a affine
encoding cipher on a 27-letter alphabet (the letters a-z and a blank).
xgb dkjvmbkffcmtkrv m lkaerask mdbmwkfmezremzkmxrcm kkmfvkrx mxgvkmaskrvsc
- 2.
- Sometime soon, you will be emailed a message encoded by an affine
matrix cipher, as well as the few letters of the message. Decrypt it.
- 3.
- Recall that a Vignère cipher can be interpreted as a Caesar-like
cipher on n-vectors, where n is the length of the key phrase. Can
any affine encipherment on digraphs (two-character codes) be interpreted as
a an affine matrix encipherment on 2-vectors? That is, suppose I encode a
message by affine enciphering on digraphs. Can I get the same crypttext
from the same plaintext using an affine matrix enciphering (using a
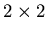 matrix) on 2-vectors?
If your answer is yes, prove it.
If no, give a counter-example that cannot be so interpreted.
matrix) on 2-vectors?
If your answer is yes, prove it.
If no, give a counter-example that cannot be so interpreted.
Scott Sutherland
1998-03-27