MAT331
Exercise 2: Some Elementary Maple

This exercise is just to demonstrate that you have paid enough attention to do some simple calculations in maple. Since maple will be our primary tool in this class, its rather important that you be able to interact with it.

Use maple to solve the following problems. Hand in a printout of your maple worksheet.

1.

Evaluate to 30 decimal places.

2.

Consider the function

2a.

Write this in a simpler form (ie, factor and reduce it).

2b.

Draw a graph of the function for 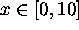. Adjust the vertical range so that some of the detail can be seen.

2c.

Compute the area of the part of the curve that lies above the x-axis and between x=0 and x=5 (i.e.\ integrate the function over the appropriate range of x values). Give your answer both in an exact form and as a decimal approximation to about 10 places.

2d.

What is the value of the integral if you remove the factor of 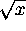from the numerator ?

2e.

Use the derivative of f(x) to determine for what real x the function has a local maximum. An approximation to about 8 decimal places is adequate.

3.

Use the commands seq and ithprime generate a list of the first 20 primes. Compute the sum of the first 20 primes, and give its integer factors.

4.

Find the solutions to the system of equations

5.

Draw a graph showing both cos(x) and its fifth taylor polynomial (that is, ) for x between -4 and 4. How many terms do you seem to need to get ``good agreement'' in this range (you will need to use something like

to make this work. See the relevant help page for more details). You should think about an appropriate way to demonstrate that the approximation you've taken is ``good''.

• About this document ...