NOTE: Each exercise is worth 10 points and can be
turned in at any time before its ``expiration date''.
At the end of the semester, I will expect you to have
turned in at least 2/5 of the exercises assigned. If you do more, I
will pick your best grades. If you do less, the missing grades will be
counted as zeros. Altogether, these will count the same as one project.
- (expires 2/11)
Use Maple to write
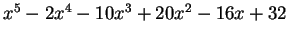 as a product of
exact linear factors. By exact, I mean you should leave any
non-rational factors expressed as radicals; do not approximate terms
like
as a product of
exact linear factors. By exact, I mean you should leave any
non-rational factors expressed as radicals; do not approximate terms
like 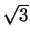 as 1.73205, etc.
as 1.73205, etc.
- (expires 2/11)
Draw a graph showing both
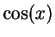 and its fifth Taylor polynomial
(that is,
and its fifth Taylor polynomial
(that is,
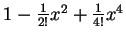 ) for
) for 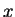 between
between 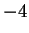 and
and
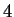 . What degree of Taylor polynomial seems to be needed to get good
agreement in this range''
Hint: use a variation of the command
convert(taylor(cos(x),x,5),polynom) to make this work. Think of a
suitable way to demonstrate that the approximation you have taken is
``good''- what is a good definition of ``good'' here?
. What degree of Taylor polynomial seems to be needed to get good
agreement in this range''
Hint: use a variation of the command
convert(taylor(cos(x),x,5),polynom) to make this work. Think of a
suitable way to demonstrate that the approximation you have taken is
``good''- what is a good definition of ``good'' here?
- (expires 2/18) Consider the planar curve
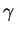 defined by
defined by
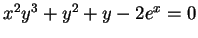 . Using only Maple, find the slope
of the tangent line to the curve at
. Using only Maple, find the slope
of the tangent line to the curve at 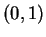 . Then plot the curve and
the tangent line on the same graph.
. Then plot the curve and
the tangent line on the same graph.
Hint: you might want to use
implicitplot from the library
plots. You might find
implicitdiff helpful, too.
- (expires 2/18)
Plot the function
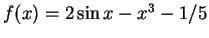 ,
for
,
for ![$x\in [-4,4]$](img12.gif) . Find all the zeros of the function with an accuracy
of 20 decimal digits. Hint: See
Digits,
fsolve.
. Find all the zeros of the function with an accuracy
of 20 decimal digits. Hint: See
Digits,
fsolve.
- (expires 2/18)
Define a Maple function
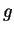 that, given a positive integer
that, given a positive integer 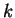 yields the sum of the first
yields the sum of the first 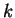 primes. What is
primes. What is 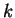 such that
such that
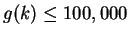 but
but
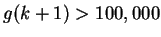 ?
You might find
sum and
ithprime helpful.
?
You might find
sum and
ithprime helpful.
- (expires 2/18)
Use the Taylor expansion of
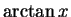 near the point
near the point 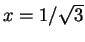 to compute the value of
to compute the value of 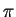 to 30 places. How many terms are
needed to compute the value to 50 places?
to 30 places. How many terms are
needed to compute the value to 50 places?
MAT 331
2002-02-10