In class, we have been discussing a system of differential equations which approximately models the flight of a glider. In this project, you are to explore a similar system, which models such a glider with a propeller or small engine attached. In this case, our model is
Here, as in class, v>0 is the speed of the glider through the air (not the horizontal speed), and ![]() is the angle the nose makes with
the horizontal direction. Note that we have fixed the drag coefficient to
be 0.3, but have added an additional term k to account for acceleration
caused by the propeller.
is the angle the nose makes with
the horizontal direction. Note that we have fixed the drag coefficient to
be 0.3, but have added an additional term k to account for acceleration
caused by the propeller.
You are to analyze and classify the solutions of this system for all
![]() (note that k=0 was covered in class). This means that you should
find the various ranges of k where the behavior is qualitatively
different.
(note that k=0 was covered in class). This means that you should
find the various ranges of k where the behavior is qualitatively
different.
Such analysis should include a discussion of the existence of fixed points (equilibrium solutions) and their linearizations (i.e., a discussion of eigenvalues and eigenvectors and how this relates to the solutions), as well as a discussion of the long-term behavior of the solutions.
In addition to the description of the trajectories in the
![]() -plane, you should also relate the solutions to properties
of glider flight. For example, discuss whether the glider eventually must
crash or can stay aloft indefinitely, whether the glider does loops, etc.
-plane, you should also relate the solutions to properties
of glider flight. For example, discuss whether the glider eventually must
crash or can stay aloft indefinitely, whether the glider does loops, etc.
- (a)
-
Find all the critical points of the system. At each critical point, calculate the corresponding linear system and find the eigenvalues of the jacobian. Then, identify the type and stability of the critical points.
- (b)
-
Use several initial data points in the first quadrant to draw the vector field and then phase portrait of the system. Identify the directions on the trajectories that correspond to time increasing.
- (c)
- Suppose the initial state of the population is given by
x(0)=2.5, y(0)=2. Find the state of the population at
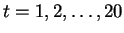 .
.
- (d)
- Explain why practically there is no ``peaceful coexistence'', i.e., with the exception of an atypical set of initial conditions (the so called separatrix curves), one or the other population must die out. For which nonzero initial populations there is no change? Sketch the separatrices, i.e., the solution curves that approach the unstable equilibrium point where both populations are positive and form the boundary between the solution curves that approach each of the two stable points where only one population survives.
Here
- (a)
- Show that the equation is rotationally invariant, i.e., if we let
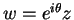 then w satisfies the same differential equation.
then w satisfies the same differential equation.
- (b)
- Plot the trajectories of the differential equation for parameter values
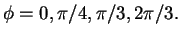 Determine the direction of the trajectories. What kind of symmetries can you see in the plots?
Determine the direction of the trajectories. What kind of symmetries can you see in the plots?
- (c)
- Can you detect, by looking at the plots above, whether the parameter
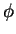 passed through a bifurcation value? What exactly is the qualitative change in the behavior of the solutions?
passed through a bifurcation value? What exactly is the qualitative change in the behavior of the solutions?
- (d)
- Estimate the actual bifurcation value of the parameter by plotting the trajectories of the system for
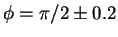 .
.
- (e)
- Let
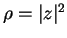 .
Notice that
.
Notice that 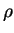 satisfies the differential equation
satisfies the differential equation
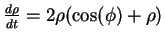 and that critical point of this differential equation corresponds to a solution of the initial one that stays fixed distance from the origin. By finding the critical points of the differential equation for
and that critical point of this differential equation corresponds to a solution of the initial one that stays fixed distance from the origin. By finding the critical points of the differential equation for 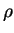 ,
explain the results of (c) and (d).
,
explain the results of (c) and (d).
- (a)
- Write a procedure that computes and draws the Julia set of the member of the family, given the value of the parameter c.
- (b)
- Compute the Julia set for the following values of the parameter:
c= .2; 1; -4+i; 1+2i.
- (c)
- Let c be real for a moment. For which c values would you expect the corresponding member of the family to have an attracting fixed point? For which c values would you expect all real numbers to have orbits that escape? Now plot the Julia set for either situation. Do you see any changes in the Julia set structure? Find the exact value of c when the bifurcation occurs.
This system is known as Lorenz system and is related to a description of 2-D flow of fluid (and things like turbulence). Study the system as deeply as you see fit, but make sure to mention the following effects that the system is notorious for: sensitive dependence of the solutions on the initial conditions (so called butterfly effect; plot some convincing graphs!) and presence of so called strange attractor, which is neither a fixed point, nor a limit cycle (again, show convincing plots). You might want to use DEplot3d alongside with DEplot.
Go to http://www.math.com/students/wonders/life/life.html and learn the rules of the Game of Life. Implement the game with Maple. Show the behavior of a few interesting objects of your choice (but do include at least Gliders and Guns!).