

Next: About this document ...
MAT 331, Spring 2000
Project 1: Dynamics of the Quadratic Map
Due Monday, April 3
In one of the most simple (discrete logistic) model of the population growth, it is assumed that size of the population in, say, a month from now is directly proportional to the current size of the population p (as the more species are around, the more will have a chance to procreate) and to (1-p) (as the habitat can't support more than certain number of species, which we assume to be equal to 1 (million, or whatever)). Thus, the dynamical system whose orbits describe the change of the size of the population in time is
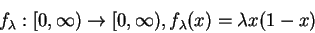
where 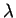 is the proportionality coefficient.
is the proportionality coefficient.
- 1.
- Find all the values of
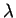 such that the corresponding population eventually dies out.
such that the corresponding population eventually dies out.
- 2.
- Find all the values of
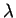 such that the corresponding population stabilizes, i.e., its size approaches certain value and stays close to it all the time.
such that the corresponding population stabilizes, i.e., its size approaches certain value and stays close to it all the time.
- 3.
- Plot the bifurcation diagram. Use it (if you want) to find the first two period doubling bifurcations. Show an attracting orbits of periods two and four. Consider an orbit asymptotic to an orbit of period two. In a couple of statements, explain the reasons of changes in the size of the corresponding population to a biologist.
- 4.
- Explain the white ``gaps'' on the bifurcation diagram (it has something to do with an attracting orbit of period three). Show a close-up of the gap.
Create an animation showing how an orbit of period three is being born. What kind of bifurcation was that? How many period three orbits are born? What kind of orbits (attracting, repelling)? Find an orbit asymptotic to an orbit of period three.
- 5.
- Finally, show a couple of orbits in the ``truly chaotic regime'' (when there are no attractors), such that their initial conditions are different by no more than 0.000001. What does this tell you about our ability to predict the population's size for the next, say, 50 years? Do you know why what you just observed is called ``butterfly effect''?


Next: About this document ...
Serge Ferleger
2000-03-11