
Next: About this document ...
MAT 331 Homework Exercises.
NOTE: Each exercise is worth 10 points and can be
turned in at any time before its ``expiration date''. You can work on
any number of the homework problems (none to all).
However, at the end of the semester, I will expect you to have
turned in at least 3/5 of the exercises assigned (approximately
10-15). If you do more, we will pick your best grades. If you do
less, the missing grades will be counted as zeros. This will determine
20% of your final grade for the class.
- #01 (exp. 01/31)
- Go to the directory mat331/Alpha in our system (mathlab.sunysb.edu)
and find the file assignment.txt in it. Read the file to learn what to do next.
- #02 (exp. 2/7)
- Use Tailor expansion for the function
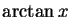 near zero at the point
near zero at the point
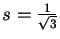 to compute
to compute 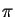 with fifty decimal digits accuracy.
with fifty decimal digits accuracy.
- #03 (exp. 2/14)
- Render (i.e., make a picture of) the Moebius strip - a one-sided nonorientable surface obtained by cutting a closed band into a single strip, giving one of the two ends thus produced a half twist, and then re-attaching the two ends. Your picture should look somewhat like this.
- #04 (exp. 2/28)
- Write a procedure firsttwodigits that returns the first two digits of its argument (which is a natural number). Use the function to compute the frequencies of each possible pair of digits that occur as the first two digits of a power of 3 (how many of the powers to consider is up to you). Finally, plot the frequencies.
- #05 (exp. 3/5)
- Let
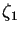 and
and 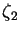 be two random variables uniformly distributed in the interval [0,1]. Using Maple, plot the density function the product of these two variables, i.e.
be two random variables uniformly distributed in the interval [0,1]. Using Maple, plot the density function the product of these two variables, i.e.
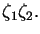 Is this product itself a uniformly distributed random variable? [Hint: First, produce the list of values (say, a thousand of them) of the product variable
Is this product itself a uniformly distributed random variable? [Hint: First, produce the list of values (say, a thousand of them) of the product variable
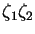 - for that, you might want to employ random[uniform] (twice). Then, use the procedure mycount from the file distribs.mws to obtain the density function out of the list of values.]
- for that, you might want to employ random[uniform] (twice). Then, use the procedure mycount from the file distribs.mws to obtain the density function out of the list of values.]
- #06 (exp. 3/5)
- [This problem is designed partly to
frustrate you and partly to show that Maple can give you trouble, even
when you do everything correctly. Hints are scattered throughout the
text.] Define
h(x) = (1+x) ex. Use Maple to evalute the following
quantities:
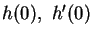 and
h''(x)-h(x). Then solve the
differential equation
and
h''(x)-h(x). Then solve the
differential equation
[It might take some time to find out how to use dsolve to
solve a differential equation with initial conditions.] If
there are no mistakes, the solution should coincide with h(x), but
it doesn't look that way, even if you simplify it! At any rate,
tell Maple to call f(x) this solution. [Cool Maple users try to
never re-type what the computer just churned out; in this case
rhs and unapply can help.] Plot f(x)-h(x),
between--say--0 and 20. What happens? Can you explain why?
- #07 (exp. 4/1)
- Data in the file mat331/Worksheets1/data.dat are coordinates of points in the plane, in the following format:
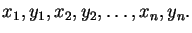 A researcher has his reason to believe that the data may be approximated well by a function of the form
y=aebx. Write Maple code that determines the best fit values for the parameters a,b. Plot the data and the function to demonstrate how well the approximation is.
A researcher has his reason to believe that the data may be approximated well by a function of the form
y=aebx. Write Maple code that determines the best fit values for the parameters a,b. Plot the data and the function to demonstrate how well the approximation is.
- #08 (exp. 4/1)
- Find a value of the parameter c such that the dynamical system
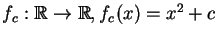 has an attracting orbit of period 6. Show the orbit, and a point whose orbit is asymptotic (is being attracted to) this periodic oribt of period 6.
has an attracting orbit of period 6. Show the orbit, and a point whose orbit is asymptotic (is being attracted to) this periodic oribt of period 6.
- #09 (exp. 4/12)
- Find all the solutions to the differential
equation
Among them, single out the one for which x(0)=3.
- #10 (exp. 4/12)
- Have Maple solve the following system of
differential equations,
with initial conditions:
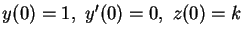 .
Let us denote
the solutions by
.
Let us denote
the solutions by
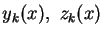 (since they depend on the parameter
k). For k taking all integer values from -10 to 10, and
(since they depend on the parameter
k). For k taking all integer values from -10 to 10, and
![$x \in
[-4,2]$](img20.gif) ,
plot on the same graph the functions yk, using a color,
and the functions zk, using a different color. [This is a
case when you don't want to retype the functions that Maple finds.]
,
plot on the same graph the functions yk, using a color,
and the functions zk, using a different color. [This is a
case when you don't want to retype the functions that Maple finds.]
- #11 (exp. 4/12)
- Find all the fixed points of the system
a fixed point being a solution for which both x(t) and y(t)
stay constant. For each of these points, describe the behavior of the
solutions that have initial conditions nearby.
- #12 (exp. 4/12)
- Consider the differential equation
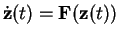 ,
where the vector
z(t)
=(x(t),y(t)) and the field
F(x,y) = (-y,x-y). Plot a few
solutions. What happens to them when
,
where the vector
z(t)
=(x(t),y(t)) and the field
F(x,y) = (-y,x-y). Plot a few
solutions. What happens to them when
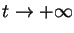 ?
Give a ``Maple-proof'' that this is a general fact for every
solution. [A ``Maple-proof'' is an argument that is rigorous once we
accept Maple results as incontrovertibly true.]
?
Give a ``Maple-proof'' that this is a general fact for every
solution. [A ``Maple-proof'' is an argument that is rigorous once we
accept Maple results as incontrovertibly true.]
- #13 (exp. 5/01)
- Suppose that the turtle is moving with constant
velocity 1 unit/sec. The turtle is told, every second, to steer right
by an amount equal to t2 degrees, where t is the time (in secs).
(For example, after the first step, it turns right 1 degree, then
after the second, turn right by 4 degrees, and so on.) Draw the curve
the tutle describes after 10 and after 100 seconds.
- #14 (exp. 5/01)
- By using only TurtleCmd, draw a random
walk of n steps. (In a random walk the turtle takes a step forward,
backwards, to the right, to the left, with equal probabilities, and then
repeats the process.) [Check rand.]
- #15 (exp. 5/01)
- Sierpinski Carpet is a fractal which is constructed analogously to the Sierpinski Sieve, but using squares instead of triangles and whose first four approximations look like this. Write a procedure that draws the n-th approximation of the Sierpinski Carpet and compute its box dimension.
- #16 (exp. 5/01)
- Find a bulb in the Mandelbrot set of the map
fc(x)=x2+c such that the orbit of zero for this map is attracted to a cycle of period three, whenever c is within the bulb. Convince yourself that this is so by trying a few different values of c from the bulb. [Some stuff from bifurcation.mws may be recycled.]


Next: About this document ...
Serge Ferleger
2000-04-15