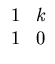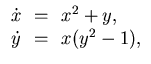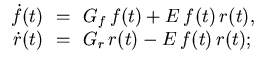MAT 331 Homework Exercises. Week 8 (Nov 9, 99).
- #26 (exp. 11/16)
- Determine the eigenvalues of
Distinguish all the possible cases (positive, negative, complex
eigenvalues) in k.
- #27 (exp. 11/16)
- For the system of differential equations of
prob. #23,
find the eigenvalues and eigenvectors of the Jacobian at the fixed points.
[This is a give-away if you have done #23.]
- #28 (exp. 11/16)
- We will study the Volterra predator-prey
equations: In a very simple ecosystem, at the time t (which is
expressed, say, in years), there is a population of f (t) foxes and
r(t) rabbits. The evolution of these quantities obeys the system
where Gf and Gr are the growth rates for the foxes and the
rabbits, respectively, in the absence of each other. E is the
probability of a fatal encounter between a fox and a rabbit
(normalized per number of foxes and rabbits).
First, write some words to explain why these equations make
sense. Then, fix Gf = 0.4, Gr = 2.4 (it's notorius that rabbits
have the tendency to reproduce quickly) and E = 0.01. For a few
initial conditions of your choice, plot the trajectories
in the (f, r)-plane (say, with
0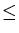 f
f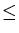 1000 and
0
1000 and
0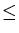 r
r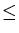 1000). For the same initial conditions, plot the actual
solutions too (i.e, f (t) against t, and r(t) against t).
Write some comments as to what happens to the two species and why.
1000). For the same initial conditions, plot the actual
solutions too (i.e, f (t) against t, and r(t) against t).
Write some comments as to what happens to the two species and why.
Finally, repeat the same procedure with
Gf = - 1.1. Things change
substantially. Again, what is the ``physical'' interpretation of this?
- #29 (exp. 11/30)
- Consider the equations of the glider with no drag
term (R = 0). Use dsolve, type=numeric to solve them numerically
with initial conditions
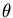 (0) = 0, v(0) = 0.8. Then solve exactly the
linearized system around the fixed point
(
(0) = 0, v(0) = 0.8. Then solve exactly the
linearized system around the fixed point
(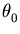 , v0) = (0, 1), with
the same initial conditions. Graph the two functions for
0
, v0) = (0, 1), with
the same initial conditions. Graph the two functions for
0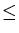 t
t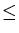 5,
and give a good estimate of their maximum difference. What happens if we
take a larger t-range?
5,
and give a good estimate of their maximum difference. What happens if we
take a larger t-range?
- #30 (exp. 11/30)
- Write a Maple procedure whose input is the pair
of functions F1, F2. With regards to the equation
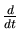 (x, y) = (F1(x, y), F2(x, y)), program the procedure to print a list of
all the real fixed points, together with the eigenvalues of the
Jacobian at each point, the eigenvectors if the eigenvalues are real, and
the nature of the fixed point (e.g., saddle point, spiraling sink,
etc.--for the trickier case of a double eigenvalue, printing
"Double eigenvalue" will suffice).
(x, y) = (F1(x, y), F2(x, y)), program the procedure to print a list of
all the real fixed points, together with the eigenvalues of the
Jacobian at each point, the eigenvectors if the eigenvalues are real, and
the nature of the fixed point (e.g., saddle point, spiraling sink,
etc.--for the trickier case of a double eigenvalue, printing
"Double eigenvalue" will suffice).
Translated from LaTeX by MAT 331
1999-11-09
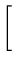
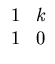
![$\displaystyle \left.\vphantom{
\begin{array}{cc}
1 & k \\
1 & 0
\end{array} }\right]$](img7.gif) .
.