MAT 331 Homework Exercises. Week 3 (Oct 5, 99).
NOTE: [No Maple] means that the problem does not involve
Maple, except as a word processor to write your solution. In this case
you can alternatively turn in a printed version, if you are more
comfortable with that.
- #11 (exp. 10/19)
- Fit the points
(1.02, - 4.30),(1.00, - 2.12),(0.99, 0.52),(1.03, 2.51),
(1.00, 3.34),(1.02, 5.30) with
a line, using the least square method we used in class. You will see
that this is not a good fit. Think of a better way to do the fit and
use Maple to do it.
- #12 (exp. 10/19)
- [No Maple] Once we have calculated the
line (or any other curve, for that matter) that best fits a sets of
points, we can get an idea how good the fit is by plotting the line
together with the points. It is much more scientific, however, to have
a measure for this. Come up with a function of the data and parameters
of a given best-fit problem that is small when the fit is good and
large when the fit is bad, no matter how many points are used.
Justify your answer.
- #13 (exp. 10/19)
- In this problem we will estimate the charge of
the electron: If an electron of energy E is thrown into a magnetic
field B, perpendicular to its velocity, its trajectory will be
deflected into a circular trajectory of radius r. The relation
between these three quantities is:
B r e = 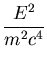 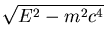 , ,
|
(1) |
where e and m are, respectively, the charge and the mass of the
electron, and c is the speed of light. The rest mass of the electron
is defined as E0 = mc2, and is about equal to
8.817 10-14Joules. In our experimental set-up the energy of the emitted
electrons is set to be
E = 2.511E0.
Use read to make Maple load and execute the commands in the file
electron_data.txt, which is located in the directories
Worksheets1 and Worksheets2 of the mat331 account.
This defines a list called electron. Each element of the list is
a pair of the form [Bi, ri], and these quantities are expressed in
Teslas and meters. Use least square fitting to determine the best value
for e. [Hint: Notice that the right hand side of (![[*]](/icons.gif/cross_ref_motif.gif) ) is
just a constant--calculate it once and for all and give it a name. Then
(
) is
just a constant--calculate it once and for all and give it a name. Then
(![[*]](/icons.gif/cross_ref_motif.gif) ) is a very easy equation, which is linear in the unknown
parameter e. To verify your solution:
e
) is a very easy equation, which is linear in the unknown
parameter e. To verify your solution:
e 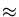 1.602 10-19 Coulomb].
1.602 10-19 Coulomb].
Physical constants courtesy of N.I.S.T.
- #14 (exp. 10/19)
- Prove relation (
![[*]](/icons.gif/cross_ref_motif.gif) ), knowing the
following physical facts: In relativistic dynamics Newton's law is
replaced by
where F is the force acting on a particle, m its mass and v, a
function of time, its velocity. In the case at hand, the force exerted
by a magnetic field B on an electron is
F = e v B/c. Recall
that in a circular motion the acceleration
a = dv/dt = v2/r, rbeing the radius of the circle. Since (
), knowing the
following physical facts: In relativistic dynamics Newton's law is
replaced by
where F is the force acting on a particle, m its mass and v, a
function of time, its velocity. In the case at hand, the force exerted
by a magnetic field B on an electron is
F = e v B/c. Recall
that in a circular motion the acceleration
a = dv/dt = v2/r, rbeing the radius of the circle. Since (![[*]](/icons.gif/cross_ref_motif.gif) ) is expressed in
terms of the energy, rather than the velocity, you also need
Einstein's formula,
) is expressed in
terms of the energy, rather than the velocity, you also need
Einstein's formula,
E = 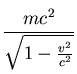 , ,
|
(3) |
which can be solved in terms of v.
- #15 (exp. 10/19)
- [No Maple] Following Section 4 of the notes, prove
that if we describe the circle of center (a, b) and radius r using
the parameters (a, b, k), with
k = a2 + b2 - r2, rather than the
more natural parameters (a, b, r), then the error function
H(a, b, k) = E(a, b,
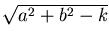 ) is quadratic in a, b and k. What does
this imply about the number of critical points?
) is quadratic in a, b and k. What does
this imply about the number of critical points?
- #16 (exp. 10/19)
- [No Maple] With reference to Problem #15, show
that, for r > 0, the transformation
(a, b, r)
 (a, b, k) is a
change of variables, that is, is one-to-one. This should help you
prove that E(a, b, r) has only one ``physical'' critical point, which
is a minimum, and is mapped, through the transformation, into the unique
critical point of H(a, b, k).
(a, b, k) is a
change of variables, that is, is one-to-one. This should help you
prove that E(a, b, r) has only one ``physical'' critical point, which
is a minimum, and is mapped, through the transformation, into the unique
critical point of H(a, b, k).
Translated from LaTeX by MAT 331
1999-10-05
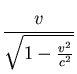
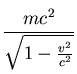 ,
,