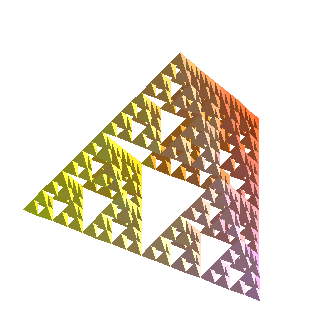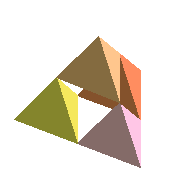
First, we define some useful routines. Tetra takes a list of the verticies of a tetrahedron, and returns a list of its faces (4 triangles).
Tetra := proc(verts)
local a,b,c,d;
a := verts[1];
b := verts[2];
c := verts[3];
d := verts[4];
RETURN( [[a,b,c], [a,b,d], [a,c,d], [b,c,d]]);
end:
Midpoint returns the midpoint of the segment joining two points.
Midpoint := proc(a,b)
RETURN( [(a[1]+b[1])/2, (a[2]+b[2])/2, (a[3]+b[3])/2]);
end:
Now for the guts.
Refine := proc (tetra)
local a,b,c,d;
a:=tetra[1];
b:=tetra[2];
c:=tetra[3];
d:=tetra[4];
RETURN( [a, Midpoint(a,b), Midpoint(a,c), Midpoint(a,d)],
[b, Midpoint(a,b), Midpoint(b,c), Midpoint(b,d)],
[c, Midpoint(c,b), Midpoint(a,c), Midpoint(c,d)],
[d, Midpoint(d,b), Midpoint(d,c), Midpoint(a,d)]);
end:
RefineAll applies Refine to each element of a list of
tetrahedra. Note that it uses map. we could have written it with
seq, but this is shorter and has the same effect.
RefineAll := proc(tlist)
RETURN(map(Refine,tlist));
end:
Recurse is a general purpose routine that computes the n-fold
composition of f applied to the second argument. that is,
f(f(f(f(...f(input)...))))
Recurse := proc(f, input, n)
if ( n <= 0) then
RETURN(input);
else
RETURN(Recurse(f, f(input), n-1));
fi;
end:
FirstT := [[-1,-1,0],[0,sqrt(3)-1,0],[1,-1,0],[0,sqrt(3)/3-1,2*sqrt(15)/5]]:Here we go. Here's the 3rd stage. (Notice that we have to map Tetra onto each element of the list that comes out of the recursion, so that we will have triangles instead of the verticies of tetrahedra.
with(plots):
setoptions3d(axes=none, scaling=constrained,shading=XY,style=patch,orientation=[60,48]);
polygonplot3d(map(Tetra,[Refine(FirstT)]),title=`Sierpinski Pyramid, level 1`);
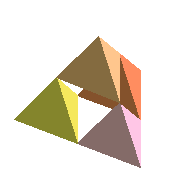
Things get a little difficult to see when you start refining, although if you make the picture in Maple and can spin it, it helps a lot. Below is level 4, and if you click on the image, you get level 5.
polygonplot3d(map(Tetra,Recurse(RefineAll,[FirstT],4)),title=`Sierpinski Pyramid, level 4`);