Math 331, Fall 2002: Problems 21-24
- 21.
- (expires 11/22) [No Maple] Compute the box counting dimension of the fractal in
the figure below:

- 22.
- (expires 11/22)
Suppose that a turtle is moving with constant
velocity 1 unit/sec. The turtle is told, every second, to steer right
by an amount equal to
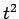 degrees, where
degrees, where 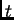 is the time (in secs).
(For example, after the first step, it turns right 1 degree, then
after the second, turn right by 4 degrees, and so on.) Draw the curve
the turtle describes after 10 and after 100 seconds.
is the time (in secs).
(For example, after the first step, it turns right 1 degree, then
after the second, turn right by 4 degrees, and so on.) Draw the curve
the turtle describes after 10 and after 100 seconds.
- 23.
- (expires 11/22)
Consider the recursively defined sequence
for 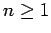 , with
, with 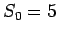 . Implement this in Maple using both a
recursive and a non-recursive procedure. [Hint for the
computation of the non-recursive formula: complete the square.]
. Implement this in Maple using both a
recursive and a non-recursive procedure. [Hint for the
computation of the non-recursive formula: complete the square.]
Bonus: rewrite the recursive procedure adding
option remember and
see the difference in terms of computational speed.
- 24.
- (expires 11/22)
By using only
TurtleCmd, draw a random
walk of
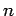 steps. (In a random walk the turtle takes a step forward,
backwards, to the right, to the left, with equal probabilities, and then
repeats the process.) [Check
rand.]
steps. (In a random walk the turtle takes a step forward,
backwards, to the right, to the left, with equal probabilities, and then
repeats the process.) [Check
rand.]
MAT 331
2002-11-13

