


Next: About this document ...
Math 331, Fall 2002: Problems 13-16
NOTE: Each exercise is worth 10 points and can be
turned in at any time before its ``expiration date''.
At the end of the semester, I will expect you to have
turned in at least 2/5 of the exercises assigned. If you do more, I
will pick your best grades. If you do less, the missing grades will be
counted as zeros. Altogether, these will count the same as one project.
- 13.
- (expires 10/20)
Find all the solutions to the differential equation
Among them, single out the one for which 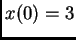 .
[Hint: read the help page for
dsolve, or just do it in your
head. It is that easy.]
.
[Hint: read the help page for
dsolve, or just do it in your
head. It is that easy.]
- 14.
- (expires 10/20)
Have Maple find analytic solutions to the following system of
differential equations,
with initial conditions:
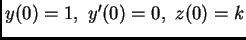 . Let us denote
the solutions by
. Let us denote
the solutions by
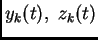 (since they depend on the parameter
(since they depend on the parameter
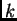 ).
).
For 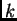 taking all integer values from -10 to 10, and
taking all integer values from -10 to 10, and ![$t \in
[-4,2]$](img7.png) , plot the functions
, plot the functions 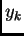 in blue, and the functions
in blue, and the functions 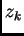 in red, all on the same graph. (Yes, you will then have 42 functions
plotted on the same graph.)
[This is certainly a case when you don't want to retype the
functions that Maple finds.
You will almost certainly need to read the help page for
dsolve.
I also found
subs,
unapply, and
seq useful.]
in red, all on the same graph. (Yes, you will then have 42 functions
plotted on the same graph.)
[This is certainly a case when you don't want to retype the
functions that Maple finds.
You will almost certainly need to read the help page for
dsolve.
I also found
subs,
unapply, and
seq useful.]
- 15.
- (expires 10/20)
For the functions
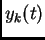 and
and 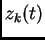 found in problem #14, plot
the parametric curves
found in problem #14, plot
the parametric curves
![$\varphi_k(t) = [y_k(t), z_k(t)]$](img12.png) for integer values of
for integer values of 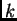 between
between
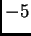 and
and 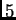 and
and 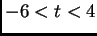 on the same graph. Use the
view
option of plot to only show what lies in the region
on the same graph. Use the
view
option of plot to only show what lies in the region
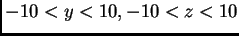 , and use a sequence of colors so that each solution is a
different color. [ HINT: you might find something like
seq(COLOR(HUE,i/11),i=0..10) useful for the latter.]
, and use a sequence of colors so that each solution is a
different color. [ HINT: you might find something like
seq(COLOR(HUE,i/11),i=0..10) useful for the latter.]
- 16.
- (expires 10/20)
Find all the fixed points of the system
a fixed point being a solution for which both 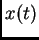 and
and 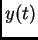 stay constant. For each of these points, describe the behavior of the
solutions that have initial conditions nearby. You can use Maple to
figure out what happens for nearby points, or you can use more
mathematical methods.
stay constant. For each of these points, describe the behavior of the
solutions that have initial conditions nearby. You can use Maple to
figure out what happens for nearby points, or you can use more
mathematical methods.
NOTE: The fact that there are various notations for
differential equations is purely intentional.



Next: About this document ...
MAT 331
2002-09-03
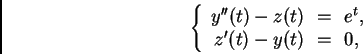
![]() taking all integer values from -10 to 10, and
taking all integer values from -10 to 10, and ![]() , plot the functions
, plot the functions ![]() in blue, and the functions
in blue, and the functions ![]() in red, all on the same graph. (Yes, you will then have 42 functions
plotted on the same graph.)
[This is certainly a case when you don't want to retype the
functions that Maple finds.
You will almost certainly need to read the help page for
dsolve.
I also found
subs,
unapply, and
seq useful.]
in red, all on the same graph. (Yes, you will then have 42 functions
plotted on the same graph.)
[This is certainly a case when you don't want to retype the
functions that Maple finds.
You will almost certainly need to read the help page for
dsolve.
I also found
subs,
unapply, and
seq useful.]
