Math 331, Fall 2002: Problems 11-12
NOTE: Each exercise is worth 10 points and can be
turned in at any time before its ``expiration date''.
At the end of the semester, I will expect you to have
turned in at least 2/5 of the exercises assigned. If you do more, I
will pick your best grades. If you do less, the missing grades will be
counted as zeros. Altogether, these will count the same as one project.
- 11.
- (expires 10/14) Following Section 4 of the notes, prove
that if we describe the circle of center
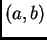 and radius
and radius 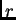 using
the parameters
using
the parameters 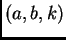 , with
, with
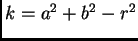 , rather than the
more natural parameters
, rather than the
more natural parameters 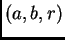 , then the error function
, then the error function
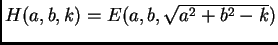 is quadratic in
is quadratic in 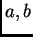 and
and 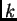 . What does
this imply about the number of critical points?
. What does
this imply about the number of critical points?
- 12.
- (expires 10/14) With reference to Problem #11, show that, for
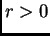 , the
transformation
, the
transformation
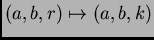 is a
valid change of variables, that is, it is one-to-one. This should help you
prove that
is a
valid change of variables, that is, it is one-to-one. This should help you
prove that 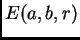 has only one ``physical'' critical point, which
is a minimum, and is mapped, through the transformation, into the unique
critical point of
has only one ``physical'' critical point, which
is a minimum, and is mapped, through the transformation, into the unique
critical point of 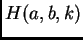 .
.
MAT 331
2002-09-25