Math 331, Fall 2002: Problems 7-10
NOTE: Each exercise is worth 10 points and can be
turned in at any time before its ``expiration date''.
At the end of the semester, I will expect you to have
turned in at least 2/5 of the exercises assigned. If you do more, I
will pick your best grades. If you do less, the missing grades will be
counted as zeros. Altogether, these will count the same as one project.
- 7.
- (expires 9/30)
Fit the points
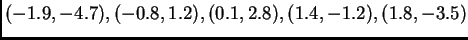 by means of a quadratic function
by means of a quadratic function
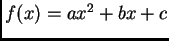 , using the least square method. First, do this
step by step, as we did in class; then, use the built-in Maple command,
described in the notes. Check that the two solutions agree.
, using the least square method. First, do this
step by step, as we did in class; then, use the built-in Maple command,
described in the notes. Check that the two solutions agree.
- 8.
- (expires 9/30)
Fit the set of points
with
a line, using the least square method we used in class. You will see
that this is not a good fit. Think of a better way to do the fit and
use Maple to do it. Explain in your solution why you think your better
way is better.
- 9.
- (expires 10/7)
[In this problem use Maple only as a word
processor. If you're more confortable with paper, you can turn in a
paper instead of a Maple worksheet.] Let
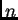 points of the form
points of the form
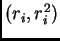 ,
,
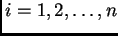 , be given. What is the quadratic
function
, be given. What is the quadratic
function
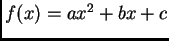 that best fits them? Prove your
answer. Does it depend on the optimization method (least square or
others)?
that best fits them? Prove your
answer. Does it depend on the optimization method (least square or
others)?
- 10.
- (expires 10/7)
Once we have calculated the
line (or any other curve, for that matter) that best fits a sets of
points, we can get an idea how good the fit is by plotting the line
together with the points. It is much more scientific, however, to have
a measure for this. Come up with a function of the data and parameters
of a given best-fit problem that is small when the fit is good and
large when the fit is bad, no matter how many points are used.
Justify your answer.
MAT 331
2002-09-25