In this note, we want to demonstrate that this vector space is the same as
the vector space of ![]() over
over ![]() (with ordinary addition and scalar
multiplication). We'll continue to use
(with ordinary addition and scalar
multiplication). We'll continue to use ![]() to represent vector
addition in
to represent vector
addition in
![]() , and
, and ![]() to represent scalar multiplication.
to represent scalar multiplication.
First, notice that if our field ![]() is the real numbers
is the real numbers ![]() , our vector
space
, our vector
space
![]() is a one-dimensional vector space, and so must be
isomorphic to
is a one-dimensional vector space, and so must be
isomorphic to ![]() with ordinary addition (since they are both finite
dimensional vector spaces over the same field and have the same dimension.)
with ordinary addition (since they are both finite
dimensional vector spaces over the same field and have the same dimension.)
To see that, let's find a basis for
![]() . Any positive real
number other than
. Any positive real
number other than ![]() will do, so let's use
will do, so let's use ![]() . To show that
. To show that ![]() is a
basis, we must prove that every other element of
is a
basis, we must prove that every other element of
![]() is a linear
combination of
is a linear
combination of ![]() . That means that given any
. That means that given any
![]() , we can find a
scalar
, we can find a
scalar
![]() for which
for which
But certainly
If we use a subfield of ![]() for
for ![]() , then depending on which
, then depending on which
![]() we choose,
we choose, ![]() may or may not be an element of
may or may not be an element of ![]() , and so we
will need more than one element in our basis for this other vector space.
For example, if
, and so we
will need more than one element in our basis for this other vector space.
For example, if
![]() , we will need an infinite basis.
, we will need an infinite basis.
The above discussion does more than show us the dimension of our vector
space. It also gives us an isomorphism between
![]() and
and ![]() . To see
this, we must verify that the map
. To see
this, we must verify that the map ![]() is one-to-one, onto, and linear.
is one-to-one, onto, and linear.
- If
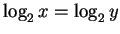 , then
, then
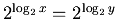 , and
so
, and
so 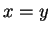 .
.
- For any
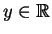 , we must find an
, we must find an
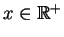 so that
so that
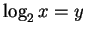 . But
. But 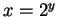 works for us here, so
works for us here, so 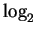 is onto.
is onto.
- At first, you might worry that the logarithm isn't a
linear map. But keep in mind that it is linear with our unusual
definition for addition and scalar multiplication. We have to show that
for any
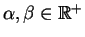 and for any
and for any
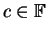 , we have
, we have
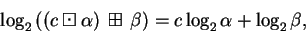
(where on the right side we are using ordinary addition and multiplication).To see that, we just expand:
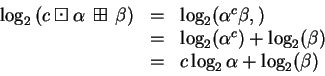
as desired.
Since we have an isomorphism between
![]() and
and ![]() , we can think of
these two vector spaces as ``the same''.
, we can think of
these two vector spaces as ``the same''.