Gram-Schmidt orthogonalization and approximation
We want to find the polynomial of degree 4 that is the best approximation to ![]() on the interval
on the interval ![]() . To do this we first take the standard basis for polynomials, {
. To do this we first take the standard basis for polynomials, {![]() } and use Gram-Schmidt to construct an orthonormal basis. While we could do this more efficiently using built-in commands of maple, we will just use maple as a calculator.
} and use Gram-Schmidt to construct an orthonormal basis. While we could do this more efficiently using built-in commands of maple, we will just use maple as a calculator.
First, we define our inner product as a function on two functions. Our inner product is the usual one, that is 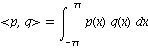 . Note that ||p-q|| is small precisely when the values of
. Note that ||p-q|| is small precisely when the values of ![]() are close to those of
are close to those of ![]() for all x in the interval
for all x in the interval ![]() .
.
For simplicity, we'll operate on expressions in ![]() rather than general functions.
rather than general functions.
| > | InnerProd:=(p,q) -> int(p*q, x=-Pi..Pi); |
![]()
We'll also want to compute the norm of our functions. However, Norm is a maple built-in function, so we'll be a little more formal and call Norm by his full name.
| > | Norman:=p->sqrt(InnerProd(p,p)); |
![]()
Now we do Gram-Schmidt to construct an orthonormal basis (with respect to this inner product) for polynomials of degree 4.
The first element of this basis is the constant function ![]() . However, we need to normalize it to be of unit length in our norm.
. However, we need to normalize it to be of unit length in our norm.
| > | f[0] := 1/Norman(1);
|
![]()
Next, we confirm that ![]() is orthogonal to
is orthogonal to ![]() . Since we want an orthonormal basis, we still want to divide
. Since we want an orthonormal basis, we still want to divide ![]() by its length
by its length
| > | InnerProd(x,f[0]); |
![]()
| > | f[1]:= x/Norman(x); |
![]()
Notice that while ![]() is orthogonal to
is orthogonal to ![]() ,
, ![]() is not.
is not.
| > | InnerProd(x^2,f[0]); |
![]()
| > | InnerProd(x^2,f[1]); |
![]()
This means we have to use Gram-Schmidt to find a function in the span of ![]() which is orthogonal to both
which is orthogonal to both ![]() and
and ![]() . Note that since
. Note that since ![]() and
and ![]() are already normalized, we don't have to divide by their lengths.
are already normalized, we don't have to divide by their lengths.
| > | ftemp:= x^2 - InnerProd(x^2,f[0])*f[0] - InnerProd(x^2,f[1])*f[1];
f[2] := collect(ftemp/Norman(ftemp),x); |
![]()
![]()
Now we play the same game with ![]() and
and ![]() . Note that if you were working these integrals out by hand, you'd quickly realize that the even powers are orthogonal to the odd ones.
. Note that if you were working these integrals out by hand, you'd quickly realize that the even powers are orthogonal to the odd ones.
| > | ftemp:= x^3 - InnerProd(x^3,f[0])*f[0] - InnerProd(x^3,f[1])*f[1] - InnerProd(x^3,f[2])*f[2]:
f[3] := collect(ftemp/Norman(ftemp),x); |
![]()
| > | ftemp:= x^4 - InnerProd(x^4,f[0])*f[0] - InnerProd(x^4,f[1])*f[1] - InnerProd(x^4,f[2])*f[2] - InnerProd(x^4,f[3])*f[3]:
f[4] := collect(ftemp/Norman(ftemp),x); |
![]()
So, we now have an orthonormal basis for fourth degree polynomials on ![]() . Just in case you are disturbed by all the
. Just in case you are disturbed by all the ![]() s and square roots, let's also write their approximate values, and also draw their graphs.
s and square roots, let's also write their approximate values, and also draw their graphs.
| > | OrthoBasis:=[f[0],f[1],f[2],f[3],f[4]]; |
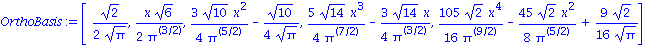
| > | evalf(OrthoBasis,4); |
![]()
| > | plot(OrthoBasis,x=-Pi..Pi, color=[black,red,blue,green,brown],thickness=2); |
![[Plot]](Gram/Gram_38.gif)
The orthonormal basis we have constructed is closely related to the Legendre polynomials, one of several families of orthogonal polynomials.
Now we can turn to our minimization problem, which becomes easy with an orthonormal basis.
Recall that the minimum with respect to our norm is just the projection of the target function onto the subspace spanned by the basis. With an orthogonal basis, this is trivial since it is just a sum of inner products times each basis element.
While we know that the inner product of ![]() with
with ![]() ,
, ![]() , and
, and ![]() is zero, we write them anyway.
is zero, we write them anyway.
| > | approx := collect(
InnerProd(cos(x),f[0])*f[0] + InnerProd(cos(x),f[1])*f[1] + InnerProd(cos(x),f[2])*f[2] + InnerProd(cos(x),f[3])*f[3] + InnerProd(cos(x),f[4])*f[4], x); evalf(approx); |
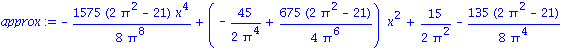
![]()
The fit is pretty good, differing by less than .07 on the whole interval.
| > | plot([cos(x),approx], x=-Pi..Pi, color=[red, green], thickness=2); |
![[Plot]](Gram/Gram_45.gif)
For comparison, let's look at the Taylor polynomial for the cosine on the same interval. Note that while the Taylor polynomial fits much better for small values, over the whole interval it is much worse.
| > | tailor:=convert(taylor(cos(x),x,5),polynom); |
| > | plot([cos(x), tailor], x=-Pi..Pi, color=[red, blue], thickness=2); |
![]()
![[Plot]](Gram/Gram_47.gif)
More explictly, we can compare the norms of the differences, and see the dramatic difference. We also show a plot of the two differences on the same axes.
| > | evalf(Norman(cos(x)-approx));
evalf(Norman(cos(x)-tailor)); |
![]()
![]()
| > | plot([cos(x)-approx, cos(x)-tailor], x=-Pi..Pi, color=[green,blue], thickness=2); |
![[Plot]](Gram/Gram_50.gif)
Just to emphasize the ease of solving the minimization problem once the basis is in hand, here are a couple more examples.
Naturally, since our basis was constructed specifically for the interval ![]() , we must work there. However, it would be not hard to adapt this same basis to work on any interval.
, we must work there. However, it would be not hard to adapt this same basis to work on any interval.
In order to avoid lots of typing, we write a Maple function that computes the inner product for us, and another that shows us the graphs.
| > | MakeApprox:=(f,basis)->collect(add(InnerProd(f,basis[i])*basis[i], i=1..nops(basis)),x):
ShowApprox:=proc(f,basis) local a; a:=MakeApprox(f,basis); print(a); print(evalf(a), " norm of difference=",evalf(Norman(a-f))); plot([f, a], x=-Pi..Pi, color=[red, green], thickness=2); end: |
First, just to check, we apply it to the same problem we just solved.
| > | ShowApprox(cos(x),OrthoBasis); |
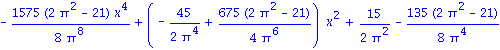
![]()
![[Plot]](Gram/Gram_54.gif)
Now we will try several other functions, just to show off. First, sin(x), which doesn't do as well (we'd need to add a fifth degree polynomial to our basis for a good fit.)
| > | ShowApprox(sin(x),OrthoBasis); |
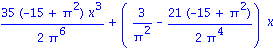
![]()
![[Plot]](Gram/Gram_57.gif)
| > | ShowApprox(cos(1+x)-x,OrthoBasis); |
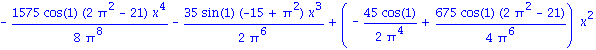
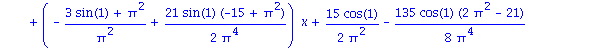
![]()
![[Plot]](Gram/Gram_61.gif)
| > | ShowApprox(exp(x)*cos(x),OrthoBasis); |
![]()
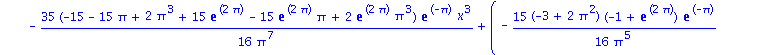
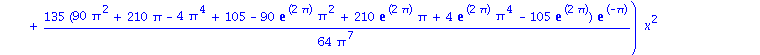
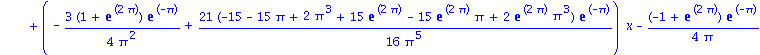
![]()
![]()
![]()
![[Plot]](Gram/Gram_69.gif)