Solutions for Second Exam Review Questions MAT 131, Fall 1998
1.
Compute the derivative with respect to
x for each of the following
expressions:
Solution:
2.
Consider the elliptic curve
C which consists of the set of points
for which
x2 -x = y3 - y
(see the graph below).
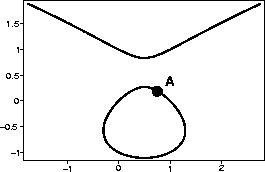
- a.
- Write the equation of the line tangent to C at the
point (1,0).
Solution:
We use implicit differentiation to obtain
2x - 1 = 3y2 y' - y'.
Solving for y' gives
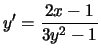 .
Plugging
in at the point (1,0) says the slope of the relevant tangent line is
.
Plugging
in at the point (1,0) says the slope of the relevant tangent line is
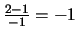 .
Thus, the line tangent to C at (1,0) is
y = 0 -1(x -1)-- that is, y=1-x.
.
Thus, the line tangent to C at (1,0) is
y = 0 -1(x -1)-- that is, y=1-x.
- b.
- Use your answer to part a to estimate the
y-coordinate of the point with x-coordinate 3/4 marked A in the
figure. Plug your estimate into the equation for C to determine
how good it is.
Solution:
Plugging
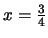 into the equation for the tangent line gives
into the equation for the tangent line gives
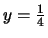 .
Trying the point
.
Trying the point
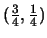 in the equation for C,
we obtain
in the equation for C,
we obtain
which is off from being true by 3/64, or about 0.0469.
- c.
- Write the equation of the parabola which best
approximates C at the point (1,0).
Solution:
We need to determine y'', so we take the derivative of y' from
part a. Again, we use implicit differentiation, this time
together with the quotient rule.
Thus,
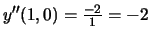 .
This means our desired parabola
is
1 - x - (x-1)2.
.
This means our desired parabola
is
1 - x - (x-1)2.
- d.
- Use your answer to part c to improve your answer
from part b. How close does this new estimate come to being
right?
Solution:
Here we obtain the estimate
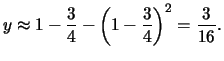 Plugging
Plugging
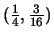 into the equation for C gives
into the equation for C gives
off by
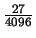 ,
or about .00659, a dramatic
improvement.
,
or about .00659, a dramatic
improvement.
3.
A mold culture is growing on the world's largest slice of bread. The
culture starts in the center of the bread, and remains approximately
circular.
- a.
- The size of the culture grows at a rate
proportional to the square of its diameter. Write a differential
equation which expresses this relationship.
Solution:
Let's let y(t) be the diameter of the culture. This changes at a
rate proportional to (that is, a constant times) its square, so we
have
y' = ky2
- b.
- Verify that
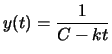 satisfies the differential
equation for any choice of k and C.
satisfies the differential
equation for any choice of k and C.
Solution:
We just need to check that this particular y(t) satisfies the
equation in a. Taking the derivative, we have
This is exactly
k (y(t))2, so the equation holds.
- c.
- If the diameter of the culture was 1 mm at 8 A.M. and
2 mm at noon, what is the size of the culture at 2 P.M.? What about at
3 P.M.? Does anything surprising happen at 4 P.M.?
Solution:
Let's let t=0 correspond to 8 A.M., so we have
That is, C=1.
Since the diameter is 2 at noon, four hours later, we have
Solving for k gives
1 - 4k = 1/2, or k=1/8, so our particular
solution is
At 2 P.M., the size of the culture is given by
y(6) = 1/(1 - 6/8) =
4, so it is 4 mm across.
At 3 P.M., the culture has a diameter of 1/(1-7/8), doubling to
8mm in one hour.
At 4 P.M., the universe comes to an end, because the size of the mold
is now infinite.
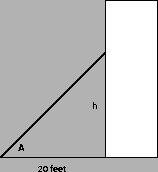
4.
A spotlight is aimed at a building whose base is 20 feet away. If
the light is raised so that its angle increases at a constant rate of
5 degrees per second, how fast is the image rising when the light
makes a 45 degree angle with the ground?
Solution:
It is helpful to draw a figure. Let's call the angle the spotlight
makes with the ground A,
so we have
Let's also call the
distance from the ground to where the spotlight hits the building h,
so what we want to know is
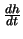 when A=45 degrees, or
when A=45 degrees, or
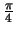 radians.
radians.
It is probably safe to assume that the building is at least
approximately perpendicular to the ground, so
Differentiating this with respect to t gives
Plugging in what we know gives the result:
or about
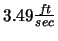 .
.
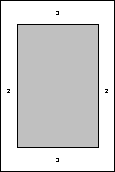
5.
A poster is to be made which requires
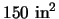 for the printed
part, and is to have a 3" margin at the top and bottom, and a 2"
margin on the sides. What should the dimensions be in order to
minimize the total area of the poster?
for the printed
part, and is to have a 3" margin at the top and bottom, and a 2"
margin on the sides. What should the dimensions be in order to
minimize the total area of the poster?
Solution:
If we let w represent the width of the printed message and h be
its height, then hw = 150, or h = 150/w. The dimensions of the
poster are 4+w wide by 6+h tall, so we want to minimize
Thus,
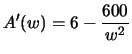 , and A'(w) = 0 when w=10.
So the dimensions of the optimal poster are
, and A'(w) = 0 when w=10.
So the dimensions of the optimal poster are
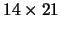 , including
the margins. The area for the message is
, including
the margins. The area for the message is
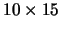 .
.
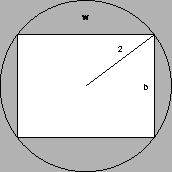
6.
The stiffness of a beam is directly proportional to the product of its
width and the cube of its breadth. What are the dimensions of the
stiffest beam that can be cut from a cylindrical log with a radius of
2'?
Solution:
We want to maximize the product w b3, where
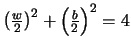 , that
is,
, that
is,
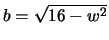 . We also must have 0 < w < 4.
. We also must have 0 < w < 4.
So,
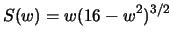 , and
, and
S' is zero when w=4 and w=2. For w=4 we have b=0, which
gives a strength of 0, as does w=0. When w=2, we have
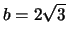 , so the optimal dimensions are
, so the optimal dimensions are
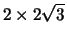 .
.
7.
At what
x value does the maximum of 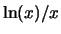 occur? What is the
maximum value of the function?
occur? What is the
maximum value of the function?
Solution:
Write
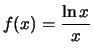 . Then
. Then
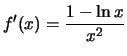 .
Thus, f'(x)=0 if
.
Thus, f'(x)=0 if 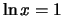 , and f'(x) does not exist if x=0.
Thus x=e is a relative maximum, and it is a global maximum because
of the shape of the graph. The maximum value is 1/e.
, and f'(x) does not exist if x=0.
Thus x=e is a relative maximum, and it is a global maximum because
of the shape of the graph. The maximum value is 1/e.
8.
Compute
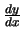 for the curve
for the curve
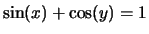 . What is
the slope of the tangent line at the point
. What is
the slope of the tangent line at the point
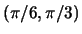 ?
?
Solution:
Using implicit differentiation,
At
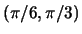 , the slope is 1.
, the slope is 1.
Scott Sutherland
1998-11-11
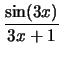
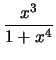
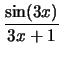
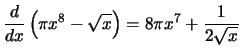
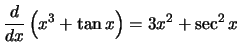
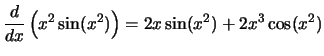
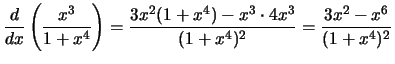
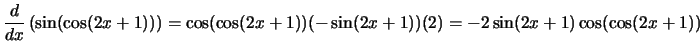
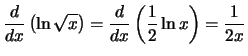
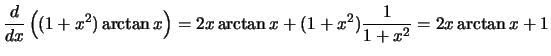
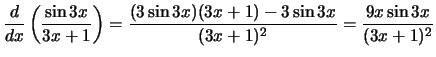
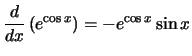
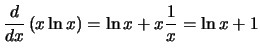

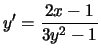 .
Plugging
in at the point (1,0) says the slope of the relevant tangent line is
.
Plugging
in at the point (1,0) says the slope of the relevant tangent line is
![]() .
Thus, the line tangent to C at (1,0) is
y = 0 -1(x -1)-- that is, y=1-x.
.
Thus, the line tangent to C at (1,0) is
y = 0 -1(x -1)-- that is, y=1-x.
![]() into the equation for the tangent line gives
into the equation for the tangent line gives
![]() .
Trying the point
.
Trying the point
![]() in the equation for C,
we obtain
in the equation for C,
we obtain
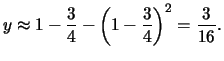 Plugging
Plugging
![]() into the equation for C gives
into the equation for C gives
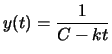 satisfies the differential
equation for any choice of k and C.
satisfies the differential
equation for any choice of k and C.
![]() for the printed
part, and is to have a 3" margin at the top and bottom, and a 2"
margin on the sides. What should the dimensions be in order to
minimize the total area of the poster?
for the printed
part, and is to have a 3" margin at the top and bottom, and a 2"
margin on the sides. What should the dimensions be in order to
minimize the total area of the poster?
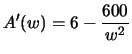 , and A'(w) = 0 when w=10.
So the dimensions of the optimal poster are
, and A'(w) = 0 when w=10.
So the dimensions of the optimal poster are
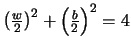 , that
is,
, that
is,
![]() , and
, and
![]() occur? What is the
maximum value of the function?
occur? What is the
maximum value of the function?
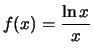 . Then
. Then
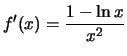 .
Thus, f'(x)=0 if
.
Thus, f'(x)=0 if ![]() , and f'(x) does not exist if x=0.
Thus x=e is a relative maximum, and it is a global maximum because
of the shape of the graph. The maximum value is 1/e.
, and f'(x) does not exist if x=0.
Thus x=e is a relative maximum, and it is a global maximum because
of the shape of the graph. The maximum value is 1/e.
![]() for the curve
for the curve
![]() . What is
the slope of the tangent line at the point
. What is
the slope of the tangent line at the point
![]() ?
?