Review for Second Exam MAT 131, Fall 1998
The midterm will be held on Tuesday, November 17 at 8:30
pm at locations to be announced.
Be sure to bring your Stony Brook ID card and your
calculator.
This handout is to help you review and study for the exam.
It includes several problems which are similar to those on the exam.
These problems are not exactly the same as those on the
exam, but they should give you an idea of the kinds of things you need
to know. However, you should also do a large number of additional
problems from the text. Do not merely limit yourself to the assigned
problems or those given here. Solutions to these problems should
appear on the web page
later this week.
The exam will cover material through section 4.3 in the
text, as well as §4.6 and §4.8.
- You should be able to take the derivative of just about any
expression consisting of standard functions. In particular, you should
know how to take the derivative of power functions, trigonometric
functions, exponentials and logarithms, and inverse trigonmetric
functions such as
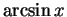 and
and 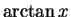 .
You also need to know
how to apply the product, quotient, and chain rules to take
derivatives of combinations of these functions.
.
You also need to know
how to apply the product, quotient, and chain rules to take
derivatives of combinations of these functions.
- You need to understand the process of implicit differentiation--
how to calculate a derivative even when one cannot explicitly solve
for y as a function of x.
- You should be able to simplify combinations of trigonmetric and
inverse trigonometric functions, such as
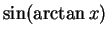 .
Do NOT
memorize these formulae-- rather, understand how to calculate
by drawing an appropriate triangle. You should also understand how to
use inverse trigonometric functions in practice.
.
Do NOT
memorize these formulae-- rather, understand how to calculate
by drawing an appropriate triangle. You should also understand how to
use inverse trigonometric functions in practice.
- You should be familiar with the idea of differential equations:
how to translate between the symbolic language of DEs and
English statements about rates of change, and how to check whether a
function is a solution of a given differential equation. You do not need to know how to find solutions, although you should know that
the solution to the equation y' = ay is of the form
y(t) = k
eat. When given a general solution to an initial value problem,
you should be able to use the initial conditions to determine the
appropriate value of the constants involved.
- You should be able to calculate the best linear approximation to
a function at a point (the tangent line), and the best quadratic
approximation. You should be able to use these to approximate
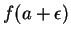 when f(a), f'(a), and possibly f''(a) are
known. You will not be asked questions on higher Taylor polynomials
or the error bounds, although understanding these ideas will only help
you.
when f(a), f'(a), and possibly f''(a) are
known. You will not be asked questions on higher Taylor polynomials
or the error bounds, although understanding these ideas will only help
you.
- You should be able to do optimization word problems and related
rates problems, determining from the English descriptions exactly what
quantities are to be found and what the relevant equations are. You
should not need to memorize any formulae,
assuming you already know the Pythagorean theorem (
a2 + b2 = c2),
how to compute the perimiter and area of a circle and a rectangle, and
how to calculate the volume of a rectangular solid.
1.
Compute the derivative with respect to
x for each of the following
expressions:
2.
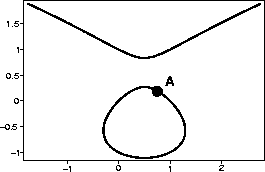
Consider the elliptic curve
C which consists of the set of points
for which
x2 -x = y3 - y
(see the graph below).
- a.
- Write the equation of the line tangent to C at the
point (1,0).
- b.
- Use your answer to part a to estimate the
y-coordinate of the point with x-coordinate 3/4 marked A in the
figure. Plug your estimate into the equation for C to determine
how good it is.
- c.
- Write the equation of the parabola which best
approximates C at the point (1,0).
- d.
- Use your answer to part c to improve your answer
from part b. How close does this new estimate come to being right?
3.
A mold culture is growing on the world's largest slice of bread. The
culture starts in the center of the bread, and remains approximately
circular.
- a.
- The size of the culture grows at a rate
proportional to the square of its diameter. Write a differential
equation which expresses this relationship.
- b.
- Verify that
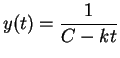 satisfies the differential
equation for any choice of k and C.
satisfies the differential
equation for any choice of k and C.
- c.
- If the diameter of the culture was 1 mm at 8 A.M. and
2 mm at noon, what is the size of the culture at 2 P.M.? What about at
3 P.M.? Does anything surprising happen at 4 P.M.?
4.
A spotlight is aimed at a building whose base is 20 feet away. If
the light is raised so that its angle increases at a constant rate of
5 degrees per second, how fast is the image rising when the light
makes a 45 degree angle with the ground?
5.
A poster is to be made which requires
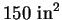 for the printed
part, and is to have a 3" margin at the top and bottom, and a 2"
margin on the sides. What should the dimensions be in order to
minimize the total area of the poster?
for the printed
part, and is to have a 3" margin at the top and bottom, and a 2"
margin on the sides. What should the dimensions be in order to
minimize the total area of the poster?
6.
The stiffness of a beam is directly proportional to the product of its
width and the cube of its breadth. What are the dimensions of the
stiffest beam that can be cut from a cylindrical log with a radius of
2'?
7.
At what
x value does the maximum of 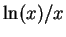 occur? What is the
maximum value of the function?
occur? What is the
maximum value of the function?
8.
Compute
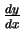 for the curve
for the curve
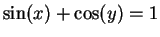 . What is
the slope of the tangent line at the point
. What is
the slope of the tangent line at the point
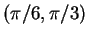 ?
?
Scott Sutherland
1998-11-11
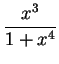
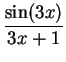
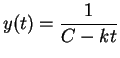 satisfies the differential
equation for any choice of k and C.
satisfies the differential
equation for any choice of k and C.
![]() for the printed
part, and is to have a 3" margin at the top and bottom, and a 2"
margin on the sides. What should the dimensions be in order to
minimize the total area of the poster?
for the printed
part, and is to have a 3" margin at the top and bottom, and a 2"
margin on the sides. What should the dimensions be in order to
minimize the total area of the poster?
![]() occur? What is the
maximum value of the function?
occur? What is the
maximum value of the function?
![]() for the curve
for the curve
![]() . What is
the slope of the tangent line at the point
. What is
the slope of the tangent line at the point
![]() ?
?