Sample First Exam        MAT 131, Fall 1998

The midterm will be held on Monday, October 19 at 8:30 pm. Be sure to bring your Stony Brook ID card and your calculator.

This sample represents the type of questions which will be on the midterm. The actual midterm will have a slightly different format, different questions, and may cover slightly different material. Just because something isn't asked here doesn't mean you aren't responsible for it. Note also that this exam may take you somewhat longer to complete than the actual exam.

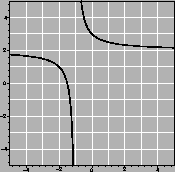
1. Consider the function $\beta(x) = x^{x}$. Write a limit which represents the value its derivative at x=2. Use your calculator to estimate $\beta'(2)$. Be sure to show your work in a clear and understandable manner.

2. In the paragraph below is a description of how the water level in a tub W(t) varied with time. Use it to draw the graph of W(t). Be sure to label any important points, and pay attention to slope, concavity, etc.

The tub held about 50 gallons of green, brackish water, with some stuff floating in it that I didn't even want to guess about. I had to get it out of there. When I opened the drain the water drained out rapidly at first, but then it went slower and slower, until it stopped completely after about 5 minutes. The tub was about 1/4-full of that nasty stuff. Would I have to stick my hand in it? Ick-- there was no way I could do that. I just stared at it for a couple of minutes, but then I got an idea. I dumped in about 10 gallons of boiling water. That did something: there was this tremendous noise like BLUUUUURP, and then the tub drained steadily, emptying completely in just a minute or so. Now all I had to do was sterilize the stupid thing before mom got home. Hmmm... should I use Lysol or gasoline?

3. The graph of a function f(x) is given below. Use it to draw the graphs of the functions g(x)=f(-x), h(x)=f^-1(x), and k(x)=2-f(x).

4. Compute the limits:          $${ \lim_{x\rightarrow 0} \frac{x^2-25}{x^2 - 5x} \qquad \lim_{x\r... ... - 25}{x^2 - 5x} \qquad \lim_{x\rightarrow +\infty} \frac{x^2-25}{x^2 - 5x} }$$

5. Write the equation of the line tangent to the function $y=x^2 - 4\sqrt{x}$ at the point (4,8).

6. A box without a top is to be made from 5 rectangular sheets of metal. If the bottom must be square and the box must have a volume of $1000\, {\rm in}^3$, what should the dimensions be in order to minimize the amount of metal needed?

7. The graph of a function f(x) is given below at the left, with a function g(x) in the middle. On the right, sketch the graph of the composition f(g(x)).

8. Sketch the graph of the derivative of the function g(x)from the previous problem.

9. In the table below, values for three functions are given, rounded to three decimal places. Determine whether each is of the form ax+b, ax²+b, or Ca^x. Then give the correct formula for f(x), g(x), and h(x).

x	1	2	3	4
f(x)	0.210	1.725	4.250	7.785
g(x)	6.462	8.573	10.684	12.795
h(x)	2.760	3.312	3.974	4.769

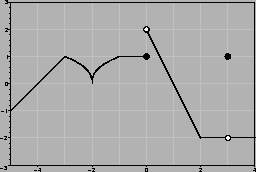
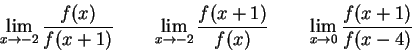
10. Write h(x) = 3x⁴ + x² + 1 as a composition of two functions f and g.

11. Use the graph of f(x) below to compute each of the following limits. If a limit does not exist, explain why.

$$\lim_{x\rightarrow 3}f(x) \qquad \lim_{x\rightarrow 0}f(x) \qquad \lim_{x\rightarrow 0+}f'(x)$$

$$\lim_{x\rightarrow -2} \frac{f(x)}{f(x+1)} \qquad \lim_{x\ri... ...1)}{f(x)} \qquad \lim_{x\rightarrow 0} \frac{f(x+1)}{f(x-4)}$$

12. Below is the graph of the derivative of a function f. The graph of f(x) is not shown. Use the graph to answer the following questions.

a.

For what set of x-values is f decreasing?

b.

For what set of x-values is the graph of f concave up?

c.

Where does f have a local maximum, if any?

d.

List all the inflection points of f, to the nearest 0.5.

e.

If f(0)=4, which of the following is the most reasonable estimate of f(-2): 2, 4, 6, or 8?

13. What is the natural domain of $f(x)=\frac{\sqrt{x+2}}{x}$?