The midterm will be held on Monday, October 19 at 8:30
pm. Be sure to bring your Stony Brook ID card and your calculator.
This sample represents the type of questions which will be on the
midterm. The actual midterm will have a slightly different format,
different questions, and may cover slightly different material. Just
because something isn't asked here doesn't mean you aren't responsible
for it. Note also that this exam may take you somewhat longer to
complete than the actual exam.
![]() . Write a limit
which represents the value its derivative at x=2. Use your
calculator to estimate
. Write a limit
which represents the value its derivative at x=2. Use your
calculator to estimate ![]() . Be sure to show your work in a
clear and understandable manner.
. Be sure to show your work in a
clear and understandable manner.
Solution:
By definition,
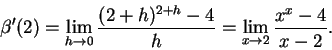
So, to approximate this, we pick several points tending towards 2, and evaluate the difference quotient at each one:
| x | 1.99 | 1.999 | 1.9999 | 2.0001 | 2.001 | 2.01 |
| xx | 3.9329427 | 3.9932341 | 3.9993228 | 4.0006773 | 4.0067793 | 4.0684040 |
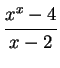 |
6.7057273 | 6.7658600 | 6.7719200 | 6.7732600 | 6.7793270 | 6.8404026 |
This approximately describes a straight line -6.695224 + 6.733987 x. Plugging in at x=2, we get 6.772749 as our estimate.
(In fact, the derivative is
![]() , so our
estimate isn't too bad).
, so our
estimate isn't too bad).
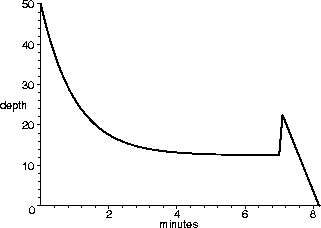
The tub held about 50 gallons of green, brackish water, with some stuff floating in it that I didn't even want to guess about. I had to get it out of there. When I opened the drain the water drained out rapidly at first, but then it went slower and slower, until it stopped completely after about 5 minutes. The tub was about 1/4-full of that nasty stuff. Would I have to stick my hand in it? Ick-- there was no way I could do that. I just stared at it for a couple of minutes, but then I got an idea. I dumped in about 10 gallons of boiling water. That did something: there was this tremendous noise like BLUUUUURP, and then the tub drained steadily, emptying completely in just a minute or so. Now all I had to do was sterilize the stupid thing before mom got home. Hmmm... should I use Lysol or gasoline?
Solution:
A graph something like the one below agrees with the description. The
graph starts out at 50, then decreases ``slower and slower'', (which
is another way of saying it is decreasing and concave up) until it
finally flattens out at about 5 minutes with a value of
![]() . The ``spike'' at around 7 minutes corresponds to
when the 10 gallons of boiling water were added, raising the amount to
. The ``spike'' at around 7 minutes corresponds to
when the 10 gallons of boiling water were added, raising the amount to
![]() , and then the level drops with constant slope, hitting
the axis just about a minute later.
, and then the level drops with constant slope, hitting
the axis just about a minute later.
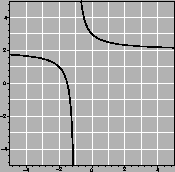
Solution:
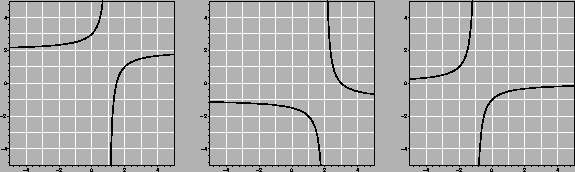
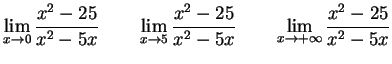
Solution:
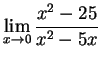 does not
exist. The numerator tends to 25, while the denominator tends
to 0. Since the denominator is positive for x<0 and negative if
x>0, the limit from below (
does not
exist. The numerator tends to 25, while the denominator tends
to 0. Since the denominator is positive for x<0 and negative if
x>0, the limit from below (
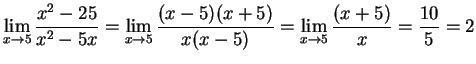 .
.
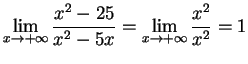 .
.
![]() at the point (4,8).
at the point (4,8).
Solution:
First, we note that
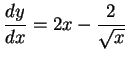 , so at the
point (4,8), the slope is
, so at the
point (4,8), the slope is
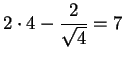 . This
means the line is
. This
means the line is
![]() , what should the dimensions be in order to
minimize the amount of metal needed?
, what should the dimensions be in order to
minimize the amount of metal needed?
Solution:
Since we are making the box from sheets of metal, if we minimize the
surface area of the box, we will minimize the amount of metal needed.
Let the base be an x by x square, and the sides be x by h. The volume of the box is h x2, so if the volume is to be 1000, we must have h = 1000/x2.
This means the surface area is given by
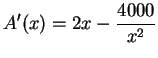 , so A'(x)=0 when
, so A'(x)=0 when
![]() . This is certainly a minimum,
since it is the only positive critical point and
. This is certainly a minimum,
since it is the only positive critical point and
![]() as
as
![]() and as
and as
![]() .
.
Thus, the minimum occurs for box with dimensions
![]() , or approximately
12.6" by 12.6" by 6.3". This requires
, or approximately
12.6" by 12.6" by 6.3". This requires
![]() (about 476.22) of sheet metal.
(about 476.22) of sheet metal.
Solution:
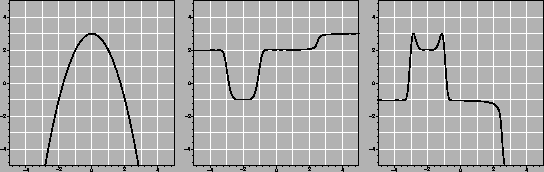
In order to figure out the above, notice that on the interval
[-5, -3.25], g is nearly constant at 2, and f(2)=-1. So ![]() is constantly -1 over this region. Similarly,
f(g([-2.5,-1.5])) = f(-1) = 2 and
f(g([-.75,2])) = f(2) = -1. Between these intervals, notice that
g(x) covers the interval [-1, 2]. Since f(0)=3, the graph of
is constantly -1 over this region. Similarly,
f(g([-2.5,-1.5])) = f(-1) = 2 and
f(g([-.75,2])) = f(2) = -1. Between these intervals, notice that
g(x) covers the interval [-1, 2]. Since f(0)=3, the graph of
![]() must go all the way up to 3 on these sections, making
Batman's ears. finally, g takes [2,3] to [2,3], which fstrecthes across [-1,-5], making Batman's shoulder. (Note that
g([3,5])=3, which f sends off the graph.)
must go all the way up to 3 on these sections, making
Batman's ears. finally, g takes [2,3] to [2,3], which fstrecthes across [-1,-5], making Batman's shoulder. (Note that
g([3,5])=3, which f sends off the graph.)
Solution:
| x | 1 | 2 | 3 | 4 |
| f(x) | 0.210 | 1.725 | 4.250 | 7.785 |
| g(x) | 6.462 | 8.573 | 10.684 | 12.795 |
| h(x) | 2.760 | 3.312 | 3.974 | 4.769 |
Solution:
Notice that
g(2)-g(1) = g(3)-g(2) = g(4)-g(3) = 2.111, so g is the
linear function, and a=2.111. So then
g(1) = 2.111 +b =6.462.
Consequently,
Note also that
h(2)/h(1) = h(3)/h(2) = h(4)/h(3) = 1.2, so h is
the exponential function, with constant a = 1.2.
Since
h(1) = C a1 = 2.760, we must have
![]() . So our exponential function is
. So our exponential function is
Finally, we probably have
f(x) = a x2 + b. If so, then
f(1) = a + b = .210 and
f(2) = 4a + b = 1.725. This means that
f(2) - f(1) = 3a = 1.515, so a=.505, and b=-.295. This gives
Solution:
Note that
h(x) = 3(x2)2 + x2 + 1. If we take g(x)=x2 and
f(x) = 3x2 + x + 1, then
f(g(x)) = h(x).
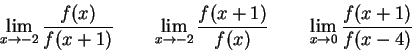
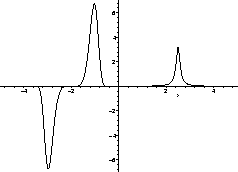
Solution:
![]() .
.
![]() does not exist, since it is 2from above and 1 from below.
does not exist, since it is 2from above and 1 from below.
![]() , because just above 0, the
graph of f is a straight line, of slope -2.
, because just above 0, the
graph of f is a straight line, of slope -2.
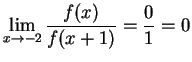 .
.
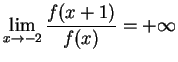 ,
because the numerator remains near 1, while the denominator gets
arbitrarily close to 0, but is always positive.
,
because the numerator remains near 1, while the denominator gets
arbitrarily close to 0, but is always positive.
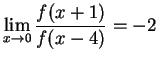 . To see
this, note that for x small,
f(x+1) = -2x and f(x-4)=x. This
means our limit becomes
. To see
this, note that for x small,
f(x+1) = -2x and f(x-4)=x. This
means our limit becomes
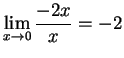 .
.
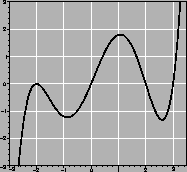
Solution:
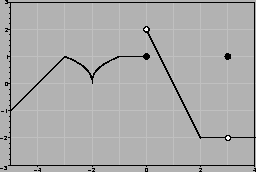
f will be decreasing whenever f' < 0, which happens for x<0 and 2<x<3.
Solution:
f is concave up whenever f''>0, that is, when f' is increasing.
This happens for x<-2,
-1.2 < x <1.1, and 2.6 < x.
Solution:
f'(2)=0, and f goes from increasing to decreasing there.
Solution:
These occur at the stationary points of f', which are,
approximately,
-2, -1.2, 1.1, and 2.6.
Solution:
The best of these is 6. To see this, note that f is decreasing
over this interval, with
-1.2 < f'(x) < 0. If f'(x) were
constantly -1.2, we would have
f(-2) = 4 + 1.2(2) = 6.4, and if
the slope were zero, we would have
f(-2) = f(0) = 4. Since the
slope is strictly between these two choices, we must have
4<f(-2)<6.4.
So 6 is the best choice.
![]() ?
?
Solution:
The largest possible domain for f(x) is
![]() or 0 < x
or 0 < x