Review for Final Exam MAT 125, Spring 1999
This is a review sheet for the final exam. The problems on
the actual final will be similar (but not identical!) to some of the
problems on this review sheet.
About 40% of the final will be material that was covered on midterms 1 and
2. Most of that material is not covered on this review sheet. You
should make sure that you understand and can do all of the problems on the
midterms, as well as the review sheets. The following additional problems
from the textbook will also be helpful:
| p. 84 (T/F) |
1, 3, 6, 8 |
| p. 84 |
2, 14, 15, 21, 24 |
| p. 182 (T/F) |
2, 3, 7, 10, 15 |
| p. 182 |
1, 7-15, 20, 27, 32, 34, 38, 46 |
| p. 260 (T/F) |
6, 8, 11 |
| p. 260 |
4-15, 27, 31, 36, 47, 49 |
| p, 292 |
5 |
Of course, you should also review the assigned homework problems.
1.
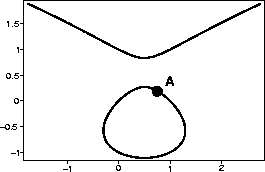
Consider the curve
C which consists of the set of points for which
x2 -x = y3 - y
(see the graph below).
- a.
- Write the equation of the line tangent to C at the
point (1,0).
- b.
- Use your answer to part a to estimate the
y-coordinate of the point with x-coordinate 3/4 marked A in the
figure. Plug your estimate into the equation for C to determine
how good it is.
2.
For each of the following functions, find the absolute maximum and
minimum values for
x in the given intervals. Also state the x value
where they occur.
- a.
-
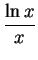 for
for
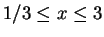 .
.
- b.
-
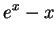 for
for
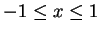 .
.
- c.
-
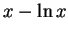 for
for
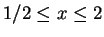 .
.
- d.
-
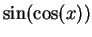 for
for
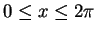 .
.
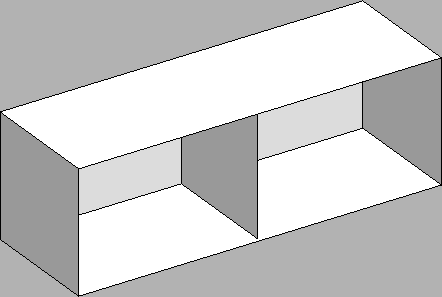
3. An open, divided box is to be constructed from three square pieces
of wood and
three rectangular ones. The rectangular pieces will be
used for the top, bottom and back,
while the squares will form the ends and the
divider.
If the total area of the wood to be used is 9 sq. ft., what are the
dimensions which will maximize the volume of the box?
4.
For the functions
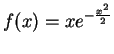 and
and
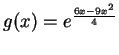 do the following:
do the following:
- a.
- Compute the first and second derivatives.
- b.
- Find the intervals on which the function is increasing and
decreasing.
- c.
- Locate all local maximima and minima.
- d.
- Locate all inflection points.
- e.
- For which x is the function concave up?
- f.
- Find all horizontal and vertical asymptotes, if any exist.
- g.
- Use the above information to sketch the graph of the function.
5.
A man starts running north at 10 km/h from a point
P. At the same time, a
car is 50 km. west of P and travels on a straight road directly east
(towards P) at 60 km/h. How fast is the distance between the jogger and
the driver changing 30 minutes later? Is the distance between them
increasing or decreasing?
6.
Find the following limits, if they exist. If the limit fails to exist,
distinguish between
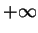 ,
, 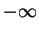 , and no limiting behavior (DNE).
, and no limiting behavior (DNE).
7.
A manufacturer wants to make a cylindrical can that has a volume of 400
cm
3. What should the radius of the base and the height be in order to
minimize the amount of material needed (that is, in order to minimize the
surface area).
What if the top and bottom of the can are cut from rectangular pieces, and
you cannot use the remaining corners for anything else?
8. Find antiderivatives for each of the following:
9. A leaky oil tanker is anchored offshore. Because the water
is very calm, the oil slick always stays circular as it expands, with
a uniform depth of 1 meter. How rapidly is oil leaking from the
tanker (in
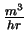 ) if the radius of the slick is expanding
at a rate of
) if the radius of the slick is expanding
at a rate of
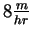 when the diameter is 20 meters?
when the diameter is 20 meters?
Scott Sutherland
1999-04-28

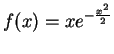 and
and
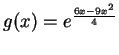 do the following:
do the following:
![]() ,
, ![]() , and no limiting behavior (DNE).
, and no limiting behavior (DNE).
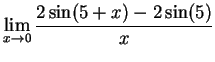
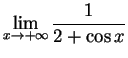
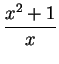
![]() ) if the radius of the slick is expanding
at a rate of
) if the radius of the slick is expanding
at a rate of
![]() when the diameter is 20 meters?
when the diameter is 20 meters?