Quiz 5         MAT 118, Spring 2003

PRINT your Name: Solution

I flip a coin 5 times in a row. The 32 possible outcomes of this are listed below.

HHHHH	HHHHT	HHHTH	HHHTT	HHTHH	HHTHT	HHTTH	HHTTT
HTHHH	HTHHT	HTHTH	HTHTT	HTTHH	HTTHT	HTTTH	HTTTT
THHHH	THHHT	THHTH	THHTT	THTHH	THTHT	THTTH	TTHHH
TTHHH	TTHHT	TTHTH	TTHTT	TTTHH	TTTHT	TTTTH	TTTTT

1. Find the probability that exactly two of the flips are heads.

   Solution: To do this, we can just count. In the above list, the possibilities with exactly two heads are in bold, and there are 10 of them. There are 32 possibilites shown, so the answer is
   

   $$\frac{10}{32} = 0.3125$$
   
   

   
   

   fill

2. Find the probability that exactly two of the flips are heads, given that the first flip is tails.

   Solution: Again, we can just count, but we have to notice WHAT we count. We are told that the first flip came up tails, so we look only at the lines where the outcomes start with a T (the bottom two lines). In those lines, there are 6 entries that have exactly two heads, out of 16 total entries. So, the probablity is
   

   $$\frac{6}{16} = 0.375$$
   
   

   
   If you prefer, you can use the conditional probability formula. In this case, it says
   

   $$P(\mbox{two heads}\vert\mbox{first is tails}) = \frac{P(\mbo... ... heads {\it and} first is tails}) } {P(\mbox{first is tails})}$$
   
   
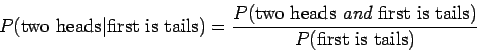
   The probability of flipping a coin five times so that you get exactly two heads and the first is flip tails is $6/32$ (again, just count: there are 32 possible flips, and 6 of them start with T and have H exactly twice). The probability that the first flip is a T is $1/2$. Thus, the probability that we have exactly two heads, if I tell you the first was T is
   
   $$\frac{6/32}{1/2} = \frac{12}{32} = \frac{6}{16}$$
   
   

   
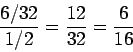
   Finally, another way to see the same result is this: since the flips are independant, when I tell you that the first was a tail, we might as well forget we did it at all. This changes the problem to ``what is the probability of flipping a coin four times and getting exactly two heads. There are six ways for this to happen (HHTT, HTHT, HTTH, THTH, THHT, TTHH), and $2^4 = 16$ possible ways for the four coin flips to turn up. Thus, again we get 6/16.

   
   

   fill