Solution:
First, we recall that for simple interest,
![]() .
In our case, we know the future value
.
In our case, we know the future value ![]() is $2400, that the annual rate is
10%, and the time is 2 years. We want to know the principle
is $2400, that the annual rate is
10%, and the time is 2 years. We want to know the principle ![]() .
Since both the rate and the time are given in years, all our units match and
there is no need for conversion. Thus, we need to solve
.
Since both the rate and the time are given in years, all our units match and
there is no need for conversion. Thus, we need to solve
for
So we need to give them $2000 now to have $2400 in two years.
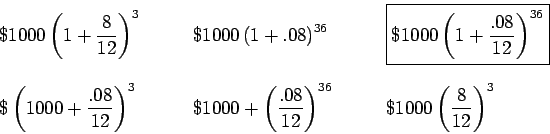
Solution:
Our principle is $1000.
Since the account is compounded monthly, our periodic interest rate is
![]() (there are 12 months in a year). We also need to express
our time in months, and 3 years is 36 months. Thus, the amount is expressed
as
(there are 12 months in a year). We also need to express
our time in months, and 3 years is 36 months. Thus, the amount is expressed
as
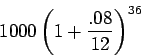
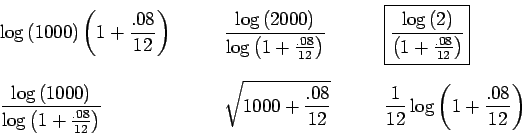
Solution:
Since we want to double our money, the future value should be $2000. As
above, the periodic rate is
![]() , the principle is $1000, and
the time is in months. Thus, we need to solve
, the principle is $1000, and
the time is in months. Thus, we need to solve
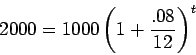
for
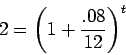
and then take the logarithm of both sides. Using the fact that
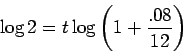
Now divide to get
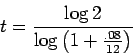
This is 104.31 months, that is, just over 8 years and 8 months.
(Note that on the original quiz, the correct answer had a typo, so everyone got full credit on this problem, no matter which choice they picked. Duh.)