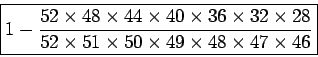
Solution: This question is almost exactly like the question on Quiz 6, and of course so is the solution.
One difference is that we want the probability of at least one pair, rather than the probability of no pairs (the other is that there are 7 cards, rather than 5). It is easiest to do this by computing the probability of no pairs, and then subtracting that result from one.
Notice that ``no pairs'' is the same as saying ``all the cards have different numbers''. So, we need to count how many ways we can pick 7 cards from a deck, all with different numbers. It is easiest if we view our hand as being ordered- that is, we distinguish the order in which we pick the cards.
First we pick the first card. There are 52 choices for this card.
For the second card, we have only 48 choices, since we cannot pick any cards which are the same number as the first. For the third card, we have 44 choices: we can't use the 4 cards that are the same number as the first card, nor the same number as the second.
Continuing in this way, we see that there are
![]() ways
to pick 7 cards with no pairs, paying attention to which is first. (If
we wanted to ignore the order, we would divide by
ways
to pick 7 cards with no pairs, paying attention to which is first. (If
we wanted to ignore the order, we would divide by ![]() ).
).
Since there are
![]() different ways to pick 7 cards, the probability of no pairs is
different ways to pick 7 cards, the probability of no pairs is
This works out to be a probability of about
- a.
- For any connected graph, a minimal spanning tree can be found
using Prim's nearest-neighbor algorithm.
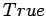 False
False - b.
- If you roll two dice, then the probability that at least one of
them is a 6 is 1/3.
True
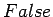
Solution: You might think this is true since the probability of rolling one die and getting a 6 is
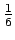 , and
, and
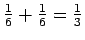 . But probabilities only add like that for mutually
exclusive events.
. But probabilities only add like that for mutually
exclusive events.
In this case, we can calculate the probability several ways. The addition rule says that it is
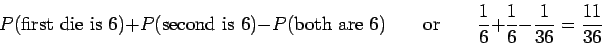
Another way is just to count that there are 11 ways for a 6 to show up on one of the two dice, and 36 possible different rolls, so again we get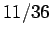 . A third way is to see that there are
. A third way is to see that there are
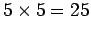 ways not to roll any sixes, so the probability is
ways not to roll any sixes, so the probability is
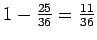 .
There are, of course, other ways to get the same answer.
.
There are, of course, other ways to get the same answer.
- c.
- Some zero-sum games have more than one equilibrium point.
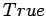 False
False - d.
- The greedy algorithm always gives the best solution to the
traveling salesman problem.
True
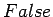
fill
Solution: For all the questions below, we will assume we can distinguish the dice, either because one is red and one is white, or we just roll one die and then the other. This means that there are always 36 different possible rolls (since a 3 on the first and a 6 on the second is different from a 6 on the first and a 3 on the second).
- a.
- What is the probability that the sum of the numbers
showing will be 2?
Solution: There is only one way to get a sum of two, by rolling two ones. Thus, the probability is
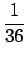 .
.
- b.
- What is the probability that the sum of the numbers
showing will be 7?
Solution: Now we have to think a little more. We can get a sum of 7 in six different ways:
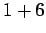 ,
, 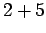 ,
, 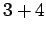 ,
, 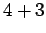 ,
, 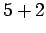 , and
, and 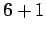 .
Thus, the probability is
.
Thus, the probability is
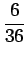 , that is
, that is
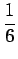 .
.
- c.
- What is the probability that the sum of the numbers
showing will be 10 or more?
Solution: To have a sum of 10 or more, we have six ways:
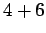 ,
, 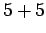 ,
, 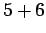 ,
, 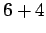 ,
, 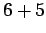 , and
, and 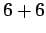 . So the probability is
. So the probability is
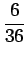 , or
, or
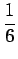 .
.
- d.
- What is the probability that the sum of the numbers
showing will be 10 or more, if you know that one of the dice shows a 5?
Solution: If you know one is a 5, then the other one must be a 5 or a 6. The probability of rolling one die and getting a 5 or a 6 is
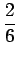 , or
, or
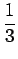 .
.
You could use conditional probability to do this, if you really wanted to.
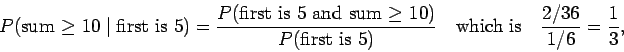
but that is more work than just doing it directly.
![\includegraphics[height=1in]{park.eps}](img45.gif)
- a.
- Draw the graph corresponding to this situation.
Solution: The graph looks pretty much like the sidewalk itself:
![\includegraphics[height=.75in]{park-graph.eps}](img38.gif)
- b.
- Is it possible for the worker cover each part of the walk
exactly once, ending up where he started? (That is, does the graph
have an Eulerian circuit?) Justify your answer.
Solution: No. To have an Eulerian circuit, all vertices must be even. But the graph in question has two odd vertices.
- c.
- Is it possible for the worker cover each part of the walk
exactly once if he doesn't need to end up where he started? (That is,
does the graph have an Eulerian path?) Justify your answer.
Solution: Yes. Since there are two odd vertices, any Eulerian path must start at one of them and end at the other. One such path is shown here.
![\includegraphics[height=1in]{park-sol.eps}](img46.gif)
| Kansas City | Omaha | St. Louis | Wichita | |
| Kansas City | -- | 220 | 225 | 280 |
| Omaha | 220 | -- | 310 | 300 |
| St. Louis | 225 | 310 | -- | 500 |
| Wichita | 280 | 300 | 500 | -- |
- a.
- Draw a weighted graph which corresponds to the situation.
![\includegraphics[height=2in]{midwest.eps}](img39.gif)
- b.
- Use the nearest neighbor algorithm to find an approximate
solution to the traveling salesman problem, making a circuit starting
at Wichita. What is the length of this circuit? (Write your answers
in the spaces below.
Solution: Using the nearest neighbor algorithm starting from Witchita, we take the shortest edge, which is the one to Kansas City at 280 miles. From Kansas City, it is slightly shorter to Omaha (220 mi). From Omaha, we must go to St. Louis (310 mi) and then return to Witchita (500 mi). This is a total of 1310 miles.
Wichita, Kansas City, Omaha, St. Louis , Wichita. Distance: 1310 miles
- c.
- Use the greedy algorithm to find an approximate
solution to the traveling salesman problem, making a circuit starting
at Wichita. What is the length of this circuit?(Write your answers
in the spaces below.
Solution: For the greedy algorithm, rather than choosing the shortest path as we go, we choose the overall shortest paths, only ruling out those that will mess us up. So, the shortest leg of the journey is KC-Omaha (220 mi) followed by KC-St. Louis (225 mi). The next shortest is Witchita-KC, but we can't use that one and still use the other two (it makes a 3-way fork). So, instead we use the Witchita-Omaha segment (300 mi). Using this rules out using the Omaha-St. Louis road, so we have to complete the journey by taking the long road from St. Louis to Witchita (500 mi). This gives an overall journey of 1245 miles, slightly shorter than the nearest neighbor algorithm does.
Wichita, Omaha, Kansas City, St. Louis, Wichita. Distance: 1245 miles
- d.
- Write the itinerary of the shortest possible
solution to the traveling salesman problem in ths case.
Solution: The only way to find the shortest possible path for the travelling salesman problem is to check ALL possible round-trip routes. Fortunately, there is only one other one (since reversing the direction doesn't change the overall distance). This is the one that avoids the Witchita-St. Louis road, and has a total distance of 1115 miles.
Wichita, Omaha, Kansas City, St. Louis, Wichita. Distance: 1115 miles
![\includegraphics[width=1.5in]{crosscam.eps}](img47.gif)
- a.
- The compressed game tree if player H goes first is shown
below. Using the game tree, indicate what strategy H should use in
order to guarantee a win, no matter what V plays. (Circle the relevant
parts of the game tree.)
![\includegraphics[width=.85\hsize]{crosscam-sol1.eps}](img43.gif)
Solution: If H moves to the center as indicated, V has no choice but to move on the end. H can then win by moving as shown, blocking any move of V's.
Note that if H plays the other possible opening move, V can respond with a winning move by placing his tile adjacent to H's.
- b.
- Even if V goes first, H can still win. Draw a partial game
tree indicating what H's winning strategy is. Note that V has two
essentially different starting moves. You must show H's response to
every move V can make, but you only have to show those for H
that result in a win for H; your goal is to describe H's winning
strategy.
Solution: V has two possible different opening moves, so we have to show H's response to each. In fact it doesn't matter what H does, but we show a possible response to each of V's moves. In both cases, V has no choice where to play following, and H always wins.
![\includegraphics[width=.75\hsize]{crosscam-sol2.eps}](img44.gif)
- a.
- This situation can be interpreted as a zero-sum game.
Summarize this information in a payoff matrix, with the Democrat as
the row player.
Solution:
- b.
- What is the best strategy for each candidate? (Find the
reduced payoff matrix.)
Solution: Since the payoff matrix is already reduced (Sorry, I goofed), there is no clear ``best stategy''. Probably the best bet here would be to use mixed strategy, where each candidate campains on domestic issues half the time and foreign policy the other half.
However, no one realized this was possible, so I pretty much accepted any reasonable choice with a decent explanation.
- c.
- If both candidates use the strategy you found above, how many
points should the Democrat rise or fall in the polls?
Solution: This depends on your answer to the previous part. Of course, your answer must be something between -2 and +4. If the mixed strategy outline above is followed, the democrat should expect to gain 2 points.
| Qatar H | Qatar L | |
| Kuwait H | (9, 9) | (5, 17) |
| Kuwait L | (17, 5) | (6, 6) |
Assuming both Kuwait and Qatar act in order to maximize their own profit, and without communicating with each other, what action will each country take, and what is their anticipated revenue? Justify your answer.
Solution: Our first step is to reduce the payoff matrix.
Note that Kuwait always prefers low prices (L), since if Qatar charges high prices, they expect to make 17 million (instead of 9 million if Kuwait charges high), and if Qatar charges low prices, Kuwait makes 6 million instead of 5 million. So we can cross out the Kuwait H row, leaving us with
| Qatar H | Qatar L | |
| Kuwait L | (17, 5) | (6, 6) |
Now Qatar also will charge low prices, since they will make 5 million if they charge high, but 6 million if they charge low. This reduces the payoff matrix to the single entry
| Qatar L | |
| Kuwait L | (6, 6) |
Thus, both countries will charge low prices, and each expects to make 6 million.