| volunteer | preferences | ||||||
| Abelard | 1 | 2 | 4 | 3 | 2 | 3 | 3 |
| Bobo | 3 | 1 | 3 | 4 | 3 | 2 | 2 |
| Cecelia | 2 | 3 | 1 | 1 | 4 | 4 | 4 |
| Duncan | 4 | 4 | 2 | 2 | 1 | 1 | 1 |
- a.
- Which volunteer would win in a plurality vote?
Solution: The tally of first-place preferences, which is all we look at in a plurality vote, is Abelard 1, Cecelia 2, Bobo 1, and Duncan 3. Thus Duncan is the winner.
- b.
- Which volunteer would win in a plurality vote with a
runoff between the top two finishers? (show your work)
Solution: The top two finishers are Cecelia and Duncan. The first four voters prefer Cecelia to Duncan, so Cecelia wins, 4 to 3.
- c.
- Which volunteer would win the Borda count? (show your work)
Solution: Recall that we give 4 points for a first-place vote, 3 for a second, 2 points for a third, and 1 point for a fourth.
- Abelard:
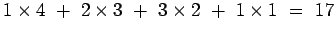
- Bobo:
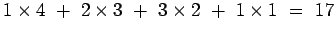
- Cecelia:
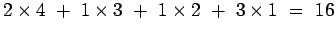
- Duncan:
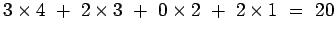
- Abelard:
- d.
- Which volunteer, if any, is the Condorcet winner? (show
your work).
Solution: We know (from part b) that Cecelia beats Duncan in a head-to-head race, so Duncan cannot be the Condorcet winner.
But Abelard beats Cecelia (4 to 3), so she is not the Condorcet winner, either.
Duncan wins against Abelard (5 to 2) and against Bobo (also 5 to 2), so neither of them can be the Condorcet winner.
Thus, there can be no Condorcet winner.
- e.
- Each club member is asked who s/he approves of for the
job, and the responses are:
Abelard & Cecelia; Abelard & Bobo; Cecelia; Cecelia & Duncan; Duncan; Duncan; Bobo & Duncan. Who wins the approval vote?Solution: Duncan gets 4 approval votes, Cecelia gets 3, Bobo 2, and Abelard 2. Thus Duncan wins the approval vote.
Solution:
This is a straightforward calculation. We are asked for the future value of
$1000 invested for 3 years. Using the formula
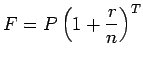 , remembering that
, remembering that ![]() is in the same
units as the compounding (so
is in the same
units as the compounding (so
![]() ), we have
), we have
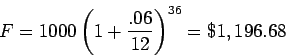
fill
Solution:
Here we are given both the present value ($1000) and the future value
($2000), and are asked to solve for the time. So, we have
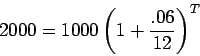
Divide both sides by 1000 to get
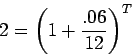
Now take the logarithm of both sides, and use a property of
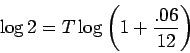
Finally, solve for
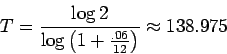
So, after 139 months (11.58 years), there will be more than $2000 in the account.
- a.
- An account earning 10% annual interest, compounded yearly.
-
 .
. - An account earning 9.75% annual interest, compounded monthly.
- c.
- An account earning 9.5% annual interest, compounded daily.
- d.
- Putting your money in a jar labelled ``magic money multiplier''.
Solution: You might be tempted to answer d., but the jar is only labelled as a magic money multipler, the label could be wrong. Or, perhaps it is right, but it multiplies the amount of money you have by zero!
So, we should check the other possibilities. We can either calculate the APY on each, or if you like, just calculate how much you would earn in a year if you invest the same amount in each.
- a.
- This compounds yearly, so its annualized yield is 10%.
- b.
- Here the APY is given by
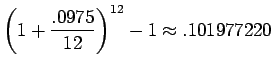 ,
that is, almost 10.2%.
,
that is, almost 10.2%.
- c.
- The APY is
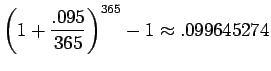 ,
or 9.96%
,
or 9.96%
- a.
- Monthly deposits of $100 at 12% annual interest, compounded monthly for 12 years.
- b.
- Monthly deposits of $200 at 6% annual interest, compounded monthly for 12 years.
-
 .
. - Monthly deposits of $100 at 6% annual interest, compounded monthly for 24 years.
Solution:
We can get a feel by just thinking a bit:
a puts in a total of
![]() ,
b puts in a total of
,
b puts in a total of
![]() , and
c puts in a total of
, and
c puts in a total of
![]() . We would
need a huge interest rate for a to come out ahead, so it is down to
b and c. But c has twice as long for the interest to
accumulate, so I expect c to be the right answer.
We can check this by explicitly calculating the accumulations.
. We would
need a huge interest rate for a to come out ahead, so it is down to
b and c. But c has twice as long for the interest to
accumulate, so I expect c to be the right answer.
We can check this by explicitly calculating the accumulations.
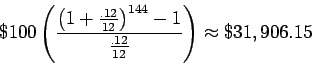
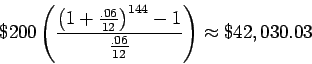
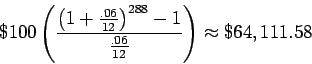
So, c is certainly the best choice.
Solution:
Note that we are given the loan amount (P) and want to calculate the regular
payment (R), so using the formula, we have
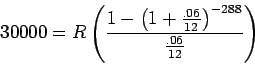
and want to solve for
so