



Next: Analysis of the Rabin
Up: Blair's Cryptography Notes
Previous: Terminology
Contents
A probabilistic test for primality
Suppose we want to test whether 247 is a prime number. Recall two facts
about prime numbers  :
:
-
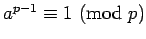 if
if
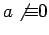 .
.
- If
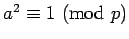 , then
, then 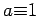 or
or 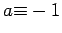 .
[
.
[
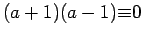 ]
]
Suppose we randomly choose 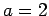 and test for consistency
with these conditions. Since
and test for consistency
with these conditions. Since
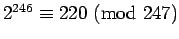 we can conclude
immediately that 247 is not a prime.
we can conclude
immediately that 247 is not a prime.
Perhaps we were lucky
with 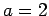 . If we try
. If we try 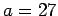 , we get
, we get
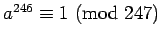 . However,
. However,
which is inconsistent with the second condition, again implying 247 is not
a prime.
Not every choice of  is inconsistent with the conditions.
For example,
is inconsistent with the conditions.
For example,
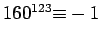 (hence
(hence
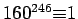 ) and
) and
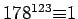 . However, the fact that some choices of
. However, the fact that some choices of  give a
proof that a number is not prime suggests the following test:
give a
proof that a number is not prime suggests the following test:
Rabin's Primality Test. Let 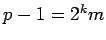 , where m is an odd number.
Choose
, where m is an odd number.
Choose  at random. Compute the sequence
at random. Compute the sequence
This sequence is consistent with  being a prime if
being a prime if 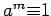 or if the sequence has
or if the sequence has 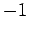 at some point,
followed by 1 for all subsequent terms. In all other cases,
at some point,
followed by 1 for all subsequent terms. In all other cases,  provides
a proof that
provides
a proof that  is not prime (this is usually described by saying that
is not prime (this is usually described by saying that
 is a witness that
is a witness that  is not prime). Repeat this test for
some number of random choices of
is not prime). Repeat this test for
some number of random choices of  , and conclude that
, and conclude that  is a prime
if none of the chosen
is a prime
if none of the chosen  is a witness.
is a witness.
Two features of the test should be emphasized. It does not provide
an absolute guarantee that  is a prime, only that it is probably a prime
(we will analyze exactly how probable in the next section). Secondly,
when we know
is a prime, only that it is probably a prime
(we will analyze exactly how probable in the next section). Secondly,
when we know  is not a prime, we do not know what its factors are--
factoring is much more difficult than testing for primality.
is not a prime, we do not know what its factors are--
factoring is much more difficult than testing for primality.
[A different
probabilistic test is described near the end of the RSA paper.]
Subsections




Next: Analysis of the Rabin
Up: Blair's Cryptography Notes
Previous: Terminology
Contents
Translated from LaTeX by Scott Sutherland
2002-12-14
![]() . If we try
. If we try ![]() , we get
, we get
![]() . However,
. However,
![]() is inconsistent with the conditions.
For example,
is inconsistent with the conditions.
For example,
![]() (hence
(hence
![]() ) and
) and
![]() . However, the fact that some choices of
. However, the fact that some choices of ![]() give a
proof that a number is not prime suggests the following test:
give a
proof that a number is not prime suggests the following test:
![]() , where m is an odd number.
Choose
, where m is an odd number.
Choose ![]() at random. Compute the sequence
at random. Compute the sequence ![]() is a prime, only that it is probably a prime
(we will analyze exactly how probable in the next section). Secondly,
when we know
is a prime, only that it is probably a prime
(we will analyze exactly how probable in the next section). Secondly,
when we know ![]() is not a prime, we do not know what its factors are--
factoring is much more difficult than testing for primality.
is not a prime, we do not know what its factors are--
factoring is much more difficult than testing for primality.